Page 90 - IJPS-7-2

International Journal of
Population Studies Modeling archaeological mortuary assemblages

et al., 2010). These distributions were utilized in the
analysis at the 5 , 50 , and 95 percentiles to account for
th
th
th
uncertainty in the expert-based judgments (Graham &
Talay, 2013). Graphically, this produced survival plots that
were visually inspected (Figures 1 and 2) to qualitatively
assess the impact of the Monte Carlo based adjustments. In
both cases, the adjusted datasets appear to be significantly
different from the observed age-distribution once the Siler
model is fit to both using maximum likelihood methods
with code custom-written in the R software package
(r-project.org). These qualitative observations suggest that
if preservation is present in these assemblages, which is
a significant likelihood, directly modeling should impact
our assessment of hypotheses.
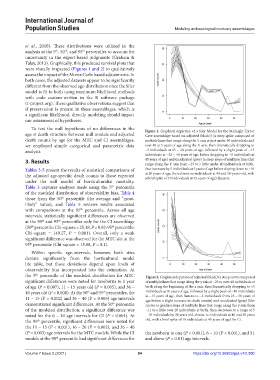
To test the null hypothesis of no differences in the Figure 1. Graphical depiction of a Siler Model for the Midnight Terror
age at death structure between null models and adjusted Cave assemblage based on adjusted (black)) (a steep spike composed of
death counts by age for the MTC and CI assemblages, multiple lines that range along the Y axis at just under 30 individuals and
we employed simple categorical and parametric data over 40 at 5 years of age along the X axis, then dramatically dropping to
analysis. ~5 individuals at 15 – 20 years of age, followed by a slight peak of ~15
individuals at ~25 – 40 years of age, before dropping to ~5 individuals at
3. Results 45 years of age) and unadjusted (grey) (a steep slope of multiple lines that
range along the Y axis from ~25 to a little under 40 individuals at birth,
Tables 3-5 present the results of statistical comparisons of that increases by 5 individuals at 5 years of age before sloping down to ~10
the adjusted age-specific death counts to those expected at 20 years of age, then almost no individuals at 40 and 50-years-old, with
a brief spike of 10 individuals at 45 years of age) datasets.
under the null model of horticulturalist mortality.
Table 3 captures analyses made using the 5 percentile
th
of the modeled distribution of observability bias, Table 4
th
those from the 50 percentile (the average and “most-
likely” value), and Table 5 reviews results associated
with comparisons at the 95 percentile. Across all age
th
intervals, statistically significant differences are observed
at the 50 and 95 percentiles only for the CI assemblage
th
th
(50 percentile: Chi-square = 25.18, P = 0.02; 95 percentile:
th
th
Chi-square = 149.27, P = 0.001). Overall, only a weak
significant difference was observed for the MTC site at the
95 percentile (Chi-square = 15.88, P = 0.1).
th
Within specific age-intervals, however, both sites
deviate significantly from the horticultural model
life table, but those deviations depend upon levels of
observability bias incorporated into the estimation. At
the 5 percentile of the modeled distribution for MTC Figure 2. Graphical depiction of adjusted (black) (a steep curve composed
th
significant differences were noted for newborns to 1 year of multiple lines that range along the y axis at ~25 to over 40 individuals at
of age (P = 0.007), 11 – 15 years old (P = 0.005), and 36 – birth along the beginning of the x axis, then dramatically dropping to <5
40 years old (P = 0.008). At the 50 and 95 percentiles, the individuals at 10 years of age, followed by a slight peak of ~10 individuals
th
th
11 – 15 (P = 0.002) and 36 – 40 (P = 0.005) age intervals at ~15 years of age, then flattens to ~3 individuals from 25 – 50 years of
age before a slight increase in death counts) and unadjusted (gray) Siler
demonstrated significant differences. At the 50 percentile curves (a gradual slope of multiple lines that range along the y axis from
th
of the modeled distribution, a significant difference was ~11 to a little over 20 individuals at birth, then decreases to a range of 5
noted for the 6 – 10 age intervals for CI (P < 0.001). At – 10 individuals by 20 years old, almost no individuals at 40 and 50 years
the 95 percentile, significant differences were noted for old, with a brief spike of 10 individuals at 45 years of age) for CI.
th
the 11 – 15 (P < 0.001), 16 – 20 (P = 0.002), and 36 – 40
(P = 0.003) age intervals for the MTC models. While the CI the newborn to one (P < 0.001), 6 – 10 (P < 0.001), and 51
models at the 95 percentile had significant differences for and above (P = 0.01) age intervals.
th
Volume 7 Issue 2 (2021) 84 https://doi.org/10.36922/ijps.v7i2.300