Page 64 - ARNM-2-4

Advances in Radiotherapy
& Nuclear Medicine Different approaches for the computation of BED

defines the DVH. From the definition of DVH, σ. Consequently, BED and the corresponding TCP are
39
 dDVH  maximized in the case of a uniform target dose. This
DVHD()− DVHD( + ∆ D) ≈−   ∆ D equals the 38
 dD  conclusion agrees with the seminal result by Webb et al.
relative volume of the target with the dose varying between that a uniform dose provides the greatest TCP for a fixed
D and D+∆D. Consequently, the average probability of integral dose in the target volume.
survival in the target can be expressed as follows: For a fixed alpha/beta ratio, BED in Eq. (12) decreases
nud
linearly with increasing α. Conversely, for a fixed α, BED
D tarmax, β D 2 d DVH nud
S mean =− ∫ exp −( α D − ) d D (10)  D 
D tarmin, N f d D approaches D mean   1+ ( α mean   as the alpha/beta ratio
)
f
In practice, the DVH for an anatomical structure is   β N  
given by a one-dimensional array: DVH(i), i = 1,…, N , increases (Figure 1).
bin
where the dose is divided into bins such that D(i) ranges
between the minimum dose D = D(1) and the maximum 2.5. Computation of BED and EQD in different TPS
2
min
dose D max = D(N ) in the structure of interest. If each bin is To determine the BED and EQD distributions in Velocity
bin
2
small enough so that dDVH ≈ DVH(i+1)−DVH(i), we can (Varian Medical Systems, Inc. Palo Alto, CA, USA) and
replace the integral in Eq. (10) with a sum. The resulting RayStation (RaySearch Laboratories, Stockholm Sweden),
equation for the average probability of survival can be these quantities are computed in each voxel of the irradiated
written as follows: structure. For the j voxel (j = 1,…, N voxel ) receiving dose
th
D , the corresponding BED is given by
N bin β Di() 2 voxel voxel
≈
S mean ∑ exp( −α D i −() )[ DVHi −() DVHi +1( )]  
i=1 N f  D j () 
(11) BED voxel j () = D voxel j ()1 + voxel  and
α
  N f( )  
2.4. Small-variance approximation  β 
Consider a treatment target with the mean dose D mean . The EQD 2, voxel j () = BED voxel j () (14)
non-uniformity of the absorbed dose in the target can be 1+ 2
α
2
2
characterized by the variance of dose σ , where σ equals the ( )
β
average of (D – D mean ) in the target volume. To elucidate the
2
dependence of BED on σ, it is useful to consider a special case
of small non-uniformity of the target dose defined by the
condition σ << D mean . Under this condition, we can express the
exponential function in Eq. (4) as a power series around D mean .
The resulting approximation for the BED is given by :
40
nud
   2 
  2 D mean  
  2 α   1 + α  
−
BED nud = D mean   1 + D mean  σ      N ( β )   
f


 ( α ) N  2  2
f
 β  − 
 α 
  N ( β )  
f
(12)
For curative treatments, the probability of survival in
the target volume must be small to achieve a TCP close to
unity. As a result, we have    
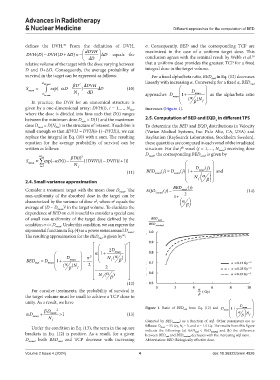
Figure 1. Ratio of BED nud from Eq. (12) and D  1+ D mean 
β D 2 mean   α  
αD mean + N mean >1 (13)     β   N f  
f
follows: D mean = 55 Gy, N f = 5, and σ = 1.5 Gy. The results from this figure
Under the condition in Eq. (13), the term in the square (denoted by BED nominal ) as a function of α/β. Other parameters are as
indicate the following: (a) BED nud < BED nominal and (b) the difference
brackets in Eq. (12) is positive. As a result, for a given between BED nud and BED nominal decreases with the increasing α/β ratio.
D mean , both BED and TCP decrease with increasing Abbreviation: BED: Biologically effective dose.
nud
Volume 2 Issue 4 (2024) 4 doi: 10.36922/arnm.4826