Page 66 - MSAM-2-1

Materials Science in Additive Manufacturing Energy absorption of Moore’s thin-walled structures

to the nature of space-filling curves and the smooth- Among all the curves, the response from LD2 for
corner design. When being compressed, some parts of the 3 order structure with 30% relative density was the
rd
the structure collided with other parts. Since Moore most jagged. To understand the reasons behind these
space-filling curves meander within a limited space, the stress drops in all the stress-strain curves, the behaviors
rd
concave and the adjacent convex tend to snap into each of the 3 order structure (30% relative density) observed
other. Due to snap-in instability, stress within the structure from the experiment are presented in Figure 7. Structural
redistributes and decreases. Instead of densification, these deformations at strains of 15%, 20%, 25%, 30%, 35%, 40%,
fractal structures utilize their compliance to endure more and 45% are displayed to provide a clearer picture of the
strain before failure. dramatic stress drops at points A, B, and C (highlighted in
When applying load from in-plane direction 2, the the stress-strain curve). From the original configuration to
structures behaved in a different way compared to LD1 a strain of 15%, the thin-walled structure contracted in a
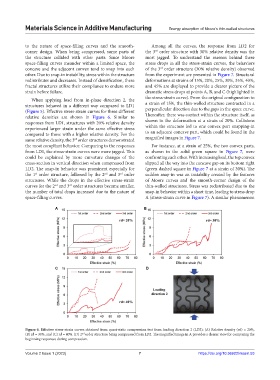
(Figure 5). Effective stress-strain curves for three different perpendicular direction due to the gaps in the space curve.
relative densities are shown in Figure 6. Similar to Thereafter, there was contact within the structure itself, as
responses from LD1, structures with 20% relative density shown in the deformation at a strain of 20%. Collisions
experienced larger strain under the same effective stress within the structure led to one convex part snapping-in
compared to those with a higher relative density. For the to an adjacent concave part, which could be found in the
same relative density, the 3 order structures demonstrated magnified images in Figure 7.
rd
the most compliant behavior. Comparing to the responses For instance, at a strain of 25%, the two convex parts,
from LD1, the stress-strain curves were more jagged. This as shown in the solid green square in Figure 7, were
could be explained by more curvature changes of the confronting each other. With increasing load, the top convex
cross-section in vertical direction when compressed from slipped all the way into the concave gap on its bottom right
LD2. The snap-in behavior was prominent especially for (green dashed square in Figure 7 at a strain of 30%). The
the 1 order structure, followed by the 2 and 3 order sudden snap-in was an instability created by the features
st
nd
rd
structures. While the drops in the effective stress-strain of Moore curves and the smooth-corner design of the
nd
rd
curves for the 2 and 3 order structures became smaller, thin-walled structures. Stress was redistributed due to the
the number of total drops increased due to the nature of snap-in behavior within a short time, leading to stress drop
space-filling curves. A (stress-strain curve in Figure 7). A similar phenomenon
A B

C D

Figure 6. Effective stress-strain curves obtained from quasi-static compression test from loading direction 2 (LD2): (A) Relative density (rd) = 20%,
(B) rd = 30%, and (C) rd = 40%. (D) 2 order structure being compressed from LD2. The magnified image in A provides a clearer view for comparing the
nd
beginning responses during compression.

Volume 2 Issue 1 (2023) 7 https://doi.org/10.36922/msam.53