Page 412 - IJB-9-3

International Journal of Bioprinting Cellular metamaterial flexure joints

A C E

B D F

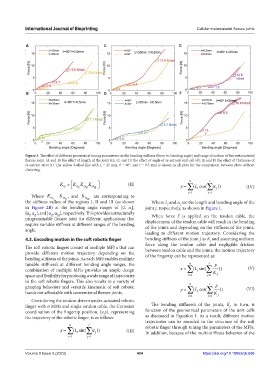
Figure 3. The effect of different geometrical tuning parameters on the bending stiffness (force vs. bending angle) and range of motion of the metamaterial
flexure joint. (A and B) the effect of length of the joint (L); (C and D) the effect of angle of re-entrant unit cell (θ); (E and F) the effect of thickness of
re-entrant strut (t). The yellow dashed line with L = 25 mm, θ = 60°, and t = 0.5 mm is shown in all plots for the comparison between plots without
cluttering.

n
i
K =   K K  II K  III   (II) y = ∑ L (cos( ∑  )) (IV)
I 

i=1 i j=1 j
Where K I  K  , and K  are corresponding to
,
III
II
the stiffness values of the regions I, II and III (as shown Where L and α are the length and bending angle of the
i
j
in Figure 2B) at the bending angle ranges of [0, α ], joint j, respectively, as shown in Figure 1.
I
[α , α ], and [α , α ], respectively. This provides a structurally When force F is applied on the tendon cable, the
III
I
II
II
programmable flexure joint for different applications that displacement of the tendon cable will result in the bending
require variable stiffness at different ranges of the bending
angle. of the joints and depending on the stiffness of the joints,
leading to different motion trajectory. Considering the
4.3. Encoding motion in the soft robotic finger bending stiffness of the joint j as K and assuming uniform
j
force along the tendon cable and negligible friction
The soft robotic fingers consist of multiple MFJ s that can between tendon cable and the joints, the motion trajectory
provide different motion trajectory depending on the of the fingertip can be represented as:
bending stiffness of the joints. As each MFJ enables multiple
tunable stiffness’s at different bending angle ranges, the n i F
i ∑
combination of multiple MFJs provides an ample design x = ∑ L (sin( K )) (V)
space and flexibility for producing a wide range of trajectories i=1 j=1 j
in the soft robotic fingers. This also results in a variety of
i
n
grasping behaviors and versatile kinematic of soft robotic y = ∑ L (cos( ∑ F )) (VI)
hands not affordable with conventional flexure joints. i K
i=1 j=1 j
Considering the tendon-driven under-actuated robotic
finger with n MFJs and single tendon cable, the Cartesian The bending stiffness’s of the joints, K, in turn, is
j
coordination of the fingertip position, (x,y), representing function of the geometrical parameters of the unit cells
the trajectory of the robotic finger, is as follows: as discussed in Equation I. As a result, different motion
trajectories can be encoded in the structure of the soft
n i robotic finger through tuning the parameters of the MFJs.
i ∑
x = ∑ L (sin(  j )) (III) In addition, because of the multi-stiffness behavior of the
i=1 j=1
Volume 9 Issue 3 (2023) 404 https://doi.org/10.18063/ijb.696