Page 36 - IJOCTA-15-1

S. Ben Hanachi, B. Sellami, M. Belloufi / IJOCTA, Vol.15, No.1, pp.25-34 (2025)
with an Intel(R) Core(TM) i3-4030U CPU @ 1.90
hyb BA HZ GHz, 4GB RAM, running Windows seven profes-
∥d ∥ ≤ ∥g k+1 ∥ + (|β | + |β |)∥d k ∥,
k+1 k k
sional.
∥s k ∥ MD
≤ Γ + M ≤ Γ + ,
λ λ
In the first set of numerical experiments, we
where present a comparison with the NDH algorithm un-
der the same conditions mentioned above. More-
over, Figures 1 and 2 show the performance pro-
2
L D 2 1
M = + files of CCH versus NDH, based on the number of
K(1 − σ)c 2 (1 − σ)Kc 2 iterations and CPU time.

σ 2
LDΓ + 2 (LD) .
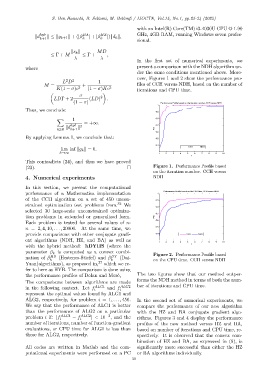
(1 − σ) Performance Profile based on the iteration number, CCH versus NDH.
1
Thus, we conclude:
0.9
1 0.8
X
= +∞.
hyb 2 0.7
∥d ∥
k≥0 k+1 P(f)
0.6
By applying Lemma 1, we conclude that: 0.5
0.4
CCH NDH
lim inf ∥g k ∥ = 0.
k→∞ 1 2 3 4 5 6 7 8 9 10
f
This contradicts (24), and thus we have proved
(23). □ Figure 1. Performance Profile based
on the iteration number. CCH versus
4. Numerical experiments NDH
In this section, we present the computational
Performance Profile based on the CPU time, CCH versus NDH.
performance of a Mathematica implementation 1
of the CCH algorithm on a set of 450 uncon- 0.9
strained optimization test problems from. 32 We
0.8
selected 30 large-scale unconstrained optimiza-
0.7
tion problems in extended or generalized form. P(f)
0.6
Each problem is tested for several values of n:
n = 2, 4, 10, . . . , 20000. At the same time, we 0.5
provide comparisons with other conjugate gradi- 0.4 CCH NDH
ent algorithms (NDH, HZ, and BA) as well as
1 2 3 4 5 6 7 8 9 10
f
with the hybrid method: hDYHS (where the
parameter β k is computed as a convex combi- Figure 2. Performance Profile based
nation of β HS (Hestenes-Stiefel) and β DY (Dai-
k k on the CPU time. CCH versus NDH
Yuan)algorithms), as proposed in, 27 which we re-
fer to here as HYB. The comparison is done using
the performance profiles of Dolan and Mor´e, The two figures show that our method outper-
forms the NDH method in terms of both the num-
The comparisons between algorithms are made
in the following context. Let f ALG1 and f ALG2 ber of iterations and CPU time.
i i
represent the optimal values found by ALG1 and
ALG2, respectively, for problem i = 1, . . . , 450. In the second set of numerical experiments, we
We say that the performance of ALG1 is better compare the performance of our new algorithm
than the performance of ALG2 on a particular with the HZ and BA conjugate gradient algo-
problem i if: |f i ALG1 − f i ALG2 | < 10 −3 , and the rithms. Figures 3 and 4 display the performance
number of iterations, number of function-gradient profiles of the new method versus HZ and BA,
evaluations, or CPU time for ALG1 is less than based on number of iterations and CPU time, re-
those for ALG2, respectively. spectively. It is observed that the convex com-
bination of HZ and BA, as expressed in (8), is
All codes are written in Matlab and the com- significantly more successful than either the HZ
putational experiments were performed on a PC or BA algorithms individually.
30