Page 82 - IJOCTA-15-2

Hybridizing biogeography-based optimization and integer programming for solving the travelling tournament ...

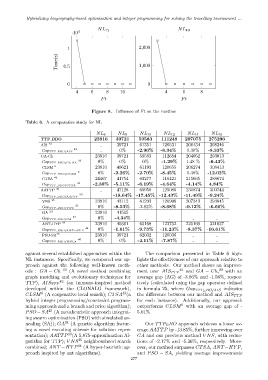
·10 4 NL 12 NL 10

1 2,000
Time(s) 0.5 1,000

0 0
4 6 8 10 4 6 8
Ft Ft

Figure 8. Influence of Ft on the runtime

Table 6. A comparative study for NL

NL 6 NL 8 NL 10 NL 12 NL 14 NL 16
TTP BBO 23916 39721 59583 111248 207075 275296
AIS 42 39721 61351 120531 206434 298246
42
Gap T T P BBO/AIS 0% -2.96% -8.34% 0.30% -8.33%
GA-Ch 23916 39721 59583 112684 204052 293013
20
Gap T T P BBO/Ch GA 0% 0% 0% -1.29% 1.48 % -6.43%
CLSM 6 23916 40621 61193 120655 206274 308413
6
Gap T T P BBO/CLSM 0% -2.26% -2.70% -8.45% 0.38% -12.02%
CTSA 43 24467 41754 63277 116421 215665 288674
43
Gap T T P BBO/CT SA -2.30% -5.11% -6.19% -4.64% -4.14% 4.84%
AATTP 30 47128 69958 125086 230874 300744
30
Gap T T P BBO/AAT T P -18.64% -17.45% -12.43% -11.49% -9.24%
VNS 25 23916 43112 61293 120906 207343 293645
25
Gap T T P BBO/V NS 0% -8.53% -2.83% -8.68% -0.12% -6.66%
GA 24 23916 41505
24
Gap T T P BBO/GA 0% -4.34%
ANT-HYP 44 23916 40361 65168 123752 225169 321037
44
Gap T T P BBO/ANT −HY P 0% -1.61% -9.73% -11.23% -8.37% -16.61%
PSO-SA 45 23916 39721 62032 120036
45
Gap T T P BBO/HHLA 0% 0% -4.11% -7.87%

against several established approaches within the The comparison presented in Table 6 high-
NL instances. Specifically, we compared our ap- lights the effectiveness of our approach relative to
proach against the following well-known meth- other methods. Our method shows an improve-
ods : GA − Ch 20 (A novel method combining ment over AIS TTP 42 and GA − Ch, 20 with an
graph matching and evolutionary techniques for average gap (AG) of -3.86% and -1.56%, respec-
42
TTP), AIS TTP (an immune-inspired method tively (calculated using the gap operator defined
developed within the CLONALG framework), in formula 25, where Gap TTP B BO/AIS indicates
6
43
CLSM (A cooperative local search); CTSA (a the difference between our method and AIS TTP
hybrid integer programming/constraint program- for each instance). Additionally, our approach
ming approach and a branch and price algorithm); outperforms CLSM 6 with an average gap of -
PSO −SA 45 (A metaheuristic approach integrat- 5.01%.
ing swarm optimization (PSO) with simulated an-
nealing (SA)); GA 24 (A genetic algorithm featur- Our TTP B BO approach achieves a lower av-
ing a novel encoding scheme for solution repre- erage AATTP by -13.85%, further improving over
30
sentation); AATTP (A 5.875-approximation Al- GA and our previous method V NS, with reduc-
gorithm for TTP); V NS 25 neighbourhood search tions of -2.17% and -5.36%, respectively. More-
combined; ANT −HY P 44 (A hyper-heuristic ap- over, our method surpasses CTSA, ANT −HY P,
proach inspired by ant algorithms). and PSO − SA, yielding average improvements
277