Page 45 - IJPS-8-2

International Journal of
Population Studies Used versus Offered densities of human population

2.5. On alternative average indicators of density

Stairs (1977) introduced generic weighting systems for
averaging the population-weighted density and measuring
the heterogeneity of human density. Denoting a weighting
system as a function x  w x() of density level x, the
associated average density is stated as follows:
E w []
x ≡ E U O w [] (21)
w
Stairs (1977) also considered “generalized population
density” as the r-th order root of the ratio of moments at
orders k + r and k:
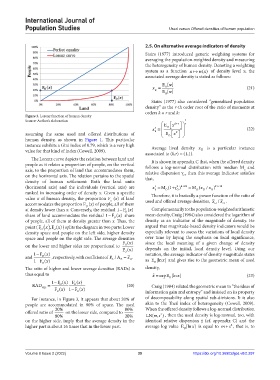
Figure 3. Lorenz function of human density
Source: Author’s elaboration 1
E x kr r
x O (22)
r
assuming the same used and offered distributions of k E O x k

human density, as shown in Figure 1. This particular
instance exhibits a Gini index of 0.79, which is a very high Average lived density x is a particular instance
value for that kind of index (Cowell, 2009). U
associated to (k,r) = (1,1).
The Lorenz curve depicts the relation between land and
It is shown in appendix C that, when the offered density
people as it relates a proportion of people, on the vertical follows a log-normal distribution with median M and
axis, to the proportion of land that accommodates them, relative dispersion γ , then this average indicator satisfies
o
on the horizontal axis. The relation pertains to the spatial that, O
density of human settlement: Both the land units
(horizontal axis) and the individuals (vertical axis) are x M(1+ 2 O ) k+r/2 M O x ( U x / O ) k r /2
r
k
O
ranked in increasing order of density x. Given a specific Therefore, it is basically a power function of the ratio of
value x of human density, the proportion F (x) of land used and offered average densities, x / x .
o
accommodates the proportion F (x) of people, all of them U O
U
at density lower than x. Conversely, the residual 1− F ()x Complementarily to the population-weighted arithmetic
O
share of land accommodates the residual 1− F ()x share mean density, Craig (1984) also considered the logarithm of
U
of people, all of them at density greater than x. Thus, the density as an indicator of the magnitude of density. He
point ( F x , F x( ) ) splits the diagram in two parts: Lower argued that magnitude-based density indicators would be
U
O
density space and people on the left side, higher density especially relevant to assess the variations of local density
space and people on the right side. The average densities over time by laying the emphasis on local significance,
on the lower and higher sides are proportional to F ()x since the local meaning of a given change of density
U
F () x depends on the initial, local density level. Using our
1− F ()x O notation, the average indicator of density magnitude states
and U , respectively, with coefficient of P / A = x .
1− F () x Z Z O as E [ln]x and gives rise to the geometric mean of used
U
O
The ratio of higher and lower average densities (RADs) is density,
thus equal to  x ≡ expE [ln x] (23)
U
1 F ()x F ()x
RAD HL | F () 1x O F () x (20) information gain and entropy” and insisted on its property
U
Craig (1984) related the geometric mean to “the ideas of
O
U
For instance, in Figure 3, it appears that about 20% of of decomposability along spatial sub-divisions. It is also
people are accommodated in 80% of space. The used akin to the Theil index of heterogeneity (Cowell, 2009).
offered ratio of 20% on the lower side, compared to 80% When the offered density follows a log-normal distribution
2
80% 20% LN(, )ms , then the used density is log-normal, too, with
on the higher side, imply that the average density in the identical relative dispersion γ (cf. appendix C) and the
higher part is about 16 times that in the lower part. average log value E [ln]x is equal to ms+ 2 , that is, to
U
Volume 8 Issue 2 (2022) 39 https://doi.org/10.36922/ijps.v8i2.297