Page 62 - IJB-10-1

International Journal of Bioprinting Microfluidic-assisted 3D bioprinting

flowing in the whole capillary without sheath under the relaxation time τ . However, there is another important
R
given pressure gradient is selected as a reference quantity: timescale, τ , which measures the typical time of the
F
dp variation of the applied stress. This could be the period of
ηˆ = η R , n , and the viscosity ratio of HB to sheath the oscillation of the stress (1/ω), if the latter is applied at
E f f
0
dz a given frequency ν = ω/2π, or to a sudden change of the
fluid is denoted X = ηˆ/η . The sheath flow rate is thus condition in the channel, e.g., a fast flow through bents
sh
Q = XQˆ [1 - R ] , with Qˆ = π/(8ηˆ)|dp/dz| R . Hence, R * I in a micromixer, a sudden stream deflection in a flow-
4
*2 2
I
sh
0
0
0
0
= R /R . The plug is found in the inner focusing junction, or an abrupt change of shear stress as
I 0 R the extrudate leaves the nozzle. On a general ground, τ =
F
region delimited by the radius R , with R = R p = σ , and the σ/(dσ/dt). The ratio of relaxation time to flow time scale τ
*
*
p
0
P
F
HB flow rate in the core is given by: 0 defines the Deborah number (De = τ /τ ), which compares
R
F
the elastic with the viscous response. The prototypal model
of a viscoelastic fluid due to Maxwell 105,108 here written for
a simple shear flow
(IV)

R t  ()V (II)
clearly shows that the behavior is viscous for τ  τ (De
R
F
The above equations can be used to design the sheath  1) while, to the opposite, it is elastic when τ  τ ,
flow: assigning R and Q determines the pressure gradient, (De  1). In fact, Equation V is unsatisfactory in many
R
F
Sh
I
*
which in its turn fixes σ = R , the plug region radius, and respects and needs to be generalized in a more complete
*
0
P
the overall core flow. form, leading to the so-called Oldroyd-B model and a
105
It is worth mentioning that yield stress and shear number of other variants, some of which with a direct
thinning behavior are not the sole fundamental rheological interpretation in terms of polymer physics. 107,109
properties of biomaterial inks. In fact, as with most Although the diffusivity of long polymers is low,
polymer-based fluids, biomaterials show viscoelastic diffusion effects may be important when different streams
responses to time-dependent flows. Indeed, due to meet in a microfluidic mixer or at flow junctions. In
106
thermal agitation, polymer chains tend to acquire a coiled addition, surface tension may play a role in extrusion,
state, thus maximizing entropy. When shear is exerted, the when the biomaterial ink encounters the external
chains get elongated, the entropy is reduced, and they react environment (air or suspension medium), while the
with an elastic force to the external action, leading to a ink wetting properties on the deposition substrate, as
time dependence of the resulting stress. described by Young’s contact angle, may be crucial for the
In elementary terms and neglecting the important actual fabrication process.
effects of chain interactions in dense suspensions, the Finally, a number of published studies include a far
107
process takes place on a typical time scale, the (principal) more detailed insight concerning the ink behavior after

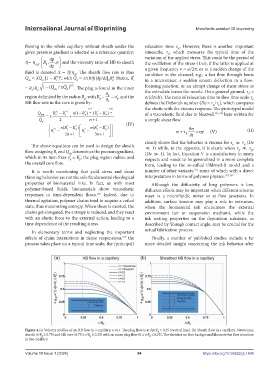
Figure 4.(a) Velocity profiles of an HB flow in a capillary, u vs.r. The plug flow is at Rp/R = 0.25 (vertical line). (b) Sheath flow in a capillary: Newtonian
0
sheath (r/R ≥ 0.75) and HB core (0.75 ≥ r/R ≥ 0.25) with an inner plug flow (0 ≤ r/R ≤ 0.25). The sketches on blue background illustrate the flow structure
0
0
0
in the capillary.
Volume 10 Issue 1 (2024) 54 https://doi.org/10.36922/ijb.1404