Page 95 - IJB-4-2

Han X, et al.

7 Pa [24] . The endothelial stimulation theory says that
when the WSS is higher than 7 Pa, it can damage the
endothelial cells during vascular remodelling while a
WSS lower than 1 Pa will form plaque due to insufficient
[24]
mechanical stimulation on endothelial cells . Therefore,
the local geometry optimisation will take place based on
the endothelial stimulation theory.
[40]
According to Khamassi et al. , the WSS in a vascular
bifurcation is related to two local parameters. They
+
are R , the asymmetry ratio and α, the total bifurcation
angle. The definition of α is shown in Figure 1(B) and R +
is calculated using equation (9):

(9)
Khamassi et al. [40] established a CFD simulation to
+
analyse how and R effect the minimal WSS at
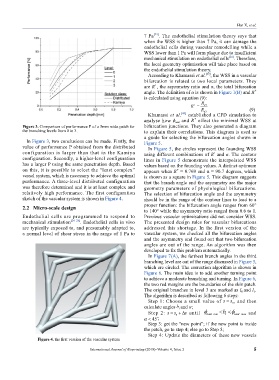
Figure 3. Comparison of performance P of a 5mm wide patch for bifurcation junctions. They also generated a diagram
the branching levels from 0 to 3. to explain their correlations. This diagram is used as
a guide for selecting the bifurcation angles shown in
In Figure 3, two conclusions can be made. Firstly, the Figure 5.
value of performance P obtained from the distributed In Figure 5, the circles represent the founding WSS
configuration is larger than that in the Kamiya using different combinations of R and α. The contour
+
configuration. Secondly, a higher-level configuration lines in Figure 5 demonstrate the interpolated WSS
has a larger P using the same penetration depth. Based values based on the founding values. A distinct optimum
on this, it is possible to select the “least complex” appears when R = 0.769 and α = 90.7 degrees, which
+
vessel system, which is necessary to achieve the optimal is shown as a square in Figure 5. This diagram suggests
performance. A three-level distributed configuration that the branch angle and the asymmetry are the major
was therefore determined and it is at least complex and geometry parameters of physiological bifurcations.
relatively high performance. The first configuration The selection of bifurcation angle and the asymmetry
sketch of the vascular system is shown in Figure 4. should be in the range of the contour lines to lead to a
2.2 Micro-scale design proper function: the bifurcation angle ranges from 60°
to 140° while the asymmetry ratio ranged from 0.6 to 1.
Endothelial cells are programmed to respond to Previous vascular optimisations did not consider WSS.
mechanical stimulation [24–26] . Endothelial cells in vivo The presented design rules for vascular bifurcations
are typically exposed to, and presumably adapted to, addressed this shortage. In the first version of the
a normal level of shear stress in the range of 1 Pa to vascular system, we checked all the bifurcation angles
and the asymmetry and found out that two bifurcation
angles are out of the range. An algorithm was then
developed to fix this problem automatically.
In Figure 7(A), the farthest branch angles in the third
branching level are out of the range discussed in Figure 5,
which are circled. The correction algorithm is shown in
Figure 6. The main idea is to add another turning point
to achieve a moderate branching and turning. In Figure 6,
the two red margins are the boundaries of the skin patch.
The original branches in level 3 are marked as l and l .
1
0
The algorithm is described as following 6 steps:
Step 1: Choose a small value of , and then
calculate angles and ;
Step 2: until and
;
Step 3: get the “new point”; if the new point is inside
the patch, go to step 4; else go to Step 5;
Step 4: Update the diameters of these new vessels
Figure 4. the first version of the vascular system

International Journal of Bioprinting (2018)–Volume 4, Issue 2 5