Page 67 - IJB-5-1

Gao D, et al.

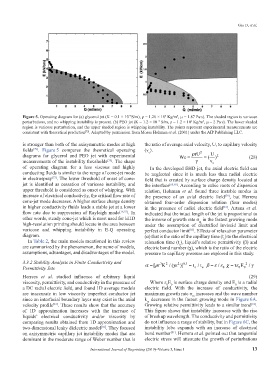
Figure 5. Operating diagram for (a) glycerol jet (K = 0.1 × 10 S/m), ρ = 1.26 × 10 Kg/m , μ = 1.87 Pa∙s). The shaded region is varicose
−5
3
3
perturbations, and no whipping instability is present. (b) PEO jet (K = 1.2 × 10 S/m, ρ = 1.2 × 10 Kg/m , μ = 2 Pa∙s). The lower shaded
−2
3
3
region is varicose perturbation, and the upper shaded region is whipping instability. The points represent experimental measurements are
consistent with theoretical prediction . Adapted by permission from Moses Hohman et al. (2001) under the AIP Publishing LLC.
[73]
is stronger than both of the axisymmetric modes at high the ratio of average axial velocity, U, to capillary velocity
fields . Figure 5 compares the theoretical operating (v ). 2
[79]
c
diagrams for glycerol and PEO jet with experimental We = ρ rU = ( U ) 2 (28)
measurements of the instability thresholds . The shape γ v c
[73]
of operating diagram for a less viscous and highly In the developed EHD jet, the axial electric field can
conducting fluids is similar to the range of cone-jet mode be neglected since it is much less than radial electric
in electrospray . The lower threshold of onset of cone- field that is created by surface charge density located at
[73]
jet is identified as cessation of varicose instability, and the interface [60,69] . According to cubic roots of dispersion
upper threshold is considered as onset of whipping. With relation, Hohman et al. found three instable modes in
increase of electrical conductivity, the critical flow rate of the presence of an axial electric field , but Herrera
[79]
cone-jet mode decreases. A higher surface charge density obtained four-order dispersion relation (four modes)
in higher conductivity fluids leads a stable jet at a lower in the presence of radial electric field . Artana et al.
[81]
flow rate due to suppression of Rayleigh mode [18,57] . In indicated that the intact length of the jet is proportional to
other words, steady cone-jet which is most used for EHD the inverse of growth rate σ in the fastest growing mode
m
high-resolution printing should locate in the area between under the assumption of electrified inviscid limit and
varicose and whipping instability in E-Q operating perfect conductor limit . Effects of relaxation parameter
[83]
diagram. (α) that is the ratio of the capillary time (t ) to the electrical
c
In Table 2, the main models mentioned in this review relaxation time (t ), liquid’s relative permittivity (β) and
e
are summarized by the phenomenon, the name of models, electric bond number (χ), which is the ratio of the electric
assumptions, advantages, and disadvantages of the model. pressure to capillary pressure are explored in this study.
3.3.2 Stability Analysis in Finite Conductivity and 3 2 2 . 0 5 / t β = ε 2 γ /
Permittivity Jets α = [ ρrK / ( γε )] = t c e ε ε/ 0 χ = rE 0
0
Herrera et al. studied influence of arbitrary liquid (29)
viscosity, permittivity, and conductivity in the presence of Where ε E is surface charge density and E is a radial
0
0
0
a DC radial electric field, and found 1D average models electric field. With the increase of conductivity, the
are inaccurate in low viscosity imperfect conductor jet maximum growth rate σ increases and the wave number
m
since an interfacial boundary layer may exist in the axial k decreases in the fastest growing mode in Figure 6A.
m
velocity profile . These results show that the accuracy Growing relative permittivity leads to a similar trend .
[81]
[81]
of 1D approximation increases with the increase of This figure shows that instability increases with the rise
liquids’ electrical conductivity and/or viscosity by of breakup wavelength. The conductivity and permittivity
comparing results obtained from 1D approximation and do not influence a range of stability, but in Figure 6C, the
two-dimensional leaky dielectric model . They focused instability lobe expands with an increase of electrical
[82]
on axisymmetric capillary jet instability modes that are bond number . Herrera et al. pointed out that tangential
[81]
dominant in the moderate range of Weber number that is electric stress will attenuate the growth of perturbations
International Journal of Bioprinting (2019)–Volume 5, Issue 1 13