Page 131 - IJOCTA-15-2

¨
E. Sonu¸c, E. Ozcan / IJOCTA, Vol.15, No.2, pp.311-329 (2025)

Parametric Analysis: UFLP

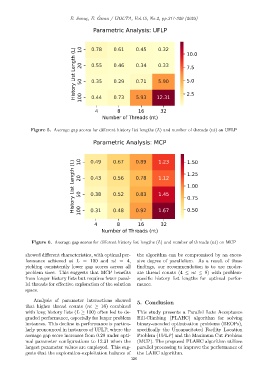
10 0.78 0.61 0.45 0.32 10.0
ength (L) 20 0.55 0.46 0.34 0.33 7.5

History List L 50 100 0.35 0.29 0.71 5.90 5.0

2.5
0.44
0.73
12.31
5.93
4 8 16 32
Number of Threads (nt)

Figure 5. Average gap scores for different history list lengths (L) and number of threads (nt) on UFLP

Parametric Analysis: MCP

10 0.49 0.67 0.89 1.23 1.50
ength (L) 20 0.43 0.56 0.78 1.12 1.25

History List L 50 100 0.38 0.52 0.83 1.45 1.00

0.75

0.50
0.48
0.31
0.92
1.67
4 8 16 32
Number of Threads (nt)

Figure 6. Average gap scores for different history list lengths (L) and number of threads (nt) on MCP

showed different characteristics, with optimal per- the algorithm can be compromised by an exces-
formance achieved at L = 100 and nt = 4, sive degree of parallelism. As a result of these
yielding consistently lower gap scores across all findings, our recommendation is to use moder-
problem sizes. This suggests that MCP benefits ate thread counts (4 ≤ nt ≤ 8) with problem-
from longer history lists but requires fewer paral- specific history list lengths for optimal perfor-
lel threads for effective exploration of the solution mance.
space.

Analysis of parameter interactions showed 5. Conclusion
that higher thread counts (nt ≥ 16) combined
with long history lists (L ≥ 100) often led to de- This study presents a Parallel Late Acceptance
graded performance, especially for larger problem Hill-Climbing (PLAHC) algorithm for solving
instances. This decline in performance is particu- binary-encoded optimization problems (BEOPs),
larly pronounced in instances of UFLP, where the specifically the Uncapacitated Facility Location
average gap score increases from 0.29 under opti- Problem (UFLP) and the Maximum Cut Problem
mal parameter configurations to 12.31 when the (MCP). The proposed PLAHC algorithm utilizes
largest parameter values are employed. This sug- parallel processing to improve the performance of
gests that the exploration-exploitation balance of the LAHC algorithm.
326