Page 139 - IJOCTA-15-2

E. Karabulut T¨urkseven, E. Gen¸c, and I. Safak / Vol.15, No.2, pp.330-342 (2025)
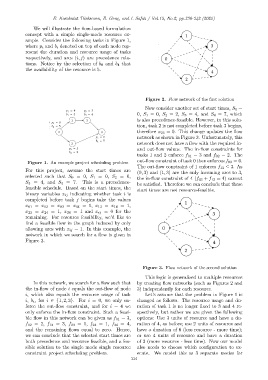
We will illustrate the flow-based formulation
concept with a simple single-mode resource ex-
ample. Consider the following tasks in Figure 1,
where p i and b i denoted on top of each node rep-
resent the duration and resource usage of tasks
respectively, and arcs (i, j) are precedence rela-
tions. Notice by the selection of b 0 and b 4 that
the availability of the resource is 5.

Figure 2. Flow network of the first solution
Now consider another set of start times, S 0 =
0, S 1 = 0, S 2 = 2, S 3 = 4, and S 4 = 7, which
is also precedence-feasible. However, in this solu-
tion, task 2 is not completed before task 3 begins,
therefore x 23 = 0. This change updates the flow
network as shown in Figure 3. Unfortunately, this
network does not have a flow with the required in-
and out-flow values. The in-flow constraints for
tasks 1 and 2 enforce f 01 = 3 and f 02 = 2. The
out-flow constraint of task 0 then enforces f 03 = 0.
Figure 1. An example project scheduling problem
The out-flow constraint of 1 enforces f 13 ≤ 3. As
For this project, assume the start times are
(0, 3) and (1, 3) are the only incoming arcs to 3,
selected such that S 0 = 0, S 1 = 0, S 2 = 0,
the in-flow constraint of 4 (f 03 + f 13 = 4) cannot
S 3 = 4, and S 4 = 7. This is a precedence-
be satisfied. Therefore we can conclude that these
feasible schedule. Based on the start times, the
start times are not resource-feasible.
binary variables x ij indicating whether task i is
completed before task j begins take the values
x 01 = x 02 = x 03 = x 04 = 1, x 13 = x 14 = 1,
x 23 = x 24 = 1, x 34 = 1 and x ij = 0 for the
remaining. For resource feasibility, we’d like to
find a feasible flow in the graph induced by only
allowing arcs with x ij = 1. In this example, the
network in which we search for a flow is given in
Figure 2.

Figure 3. Flow network of the second solution
This logic is generalized to multiple resources
In this network, we search for a flow such that by creating flow networks (such as Figures 2 and
the in-flow of node i equals the out-flow of node 3) independently for each resource.
i, which also equals the resource usage of task Let’s assume that the problem in Figure 1 is
i, b i , for i ∈ {1, 2, 3}. For i = 0, we only en- changed as follows. The resource usage and du-
force the out-flow constraint, and for i = 4 we ration of task 1 is no longer fixed to 3 and 4 re-
only enforce the in-flow constraint. Such a feasi- spectively, but rather we are given the following
ble flow in this network can be given as f 01 = 3, options: Use 3 units of resource and have a du-
f 02 = 2, f 13 = 3, f 23 = 1, f 24 = 1, f 34 = 4, ration of 4, as before; use 2 units of resource and
and the remaining flows equal to zero. Hence, have a duration of 6 (less resource - more time);
we can conclude that the selected start times are or use 4 units of resource and have a duration
both precedence and resource feasible, and a fea- of 3 (more resource - less time). Now our model
sible solution to the single mode single resource also needs to choose which configuration to ex-
constraint project scheduling problem. ecute. We model this as 3 separate modes for
334