Page 91 - IJOCTA-15-2

¨
M. Yavuz, M. Ozt¨urk, B. Ya¸skıran / IJOCTA, Vol.15, No.2, pp.281-293 (2025)
Table 1. 2-DOF robot manipulator parameters

2
Mass,M (kg) Length(m) Initial position,θ Desired path,θ d Gravity,g (m/s )
Link 1 M 1 = 1 L 1 = 1 θ 1 = π θ d1 = sin(t) 9.81
4
Link 2 M 2 = 1 L 2 = 1 θ 2 = π θ d2 = sin(t) 9.81
2
4. Results and discussion

In this section, the performance of the classi-
cal sliding mode controller and Caputo fractional
order sliding mode controllers using 3 different
sliding surface approaches are compared to each
other. The simulation was carried out in MAT-
LAB in the [0 3] time span. The trapezoid rule
is used in simulations for numerical calculations
because of its simplicity. Numerical step size is
chosen as 10 −2 . The step size is chosen highly con-
sidering the operating frequency of real systems.
The CFOSMC controller parameters are chosen
as k r = 10, µ = 1, β = 1 and α = 0.1, 0.5, 0.9.
The robot parameters are given in Table (1).

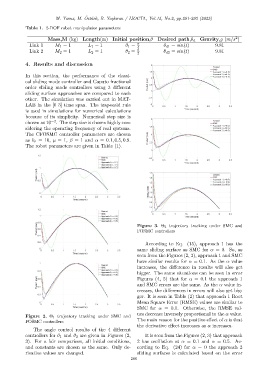
Figure 3. Θ 2 trajectory tracking under SMC and
FOSMC controllers

According to Eq. (15), approach 1 has the
same sliding surface as SMC for α = 0. So, as
seen from the Figures (2, 3), approach 1 and SMC
have similar results for α = 0.1. As the α value
increases, the difference in results will also get
bigger. The same situations can be seen in error
Figures (4, 5) that for α = 0.1 the approach 1
and SMC errors are the same. As the α value in-
creases, the differences in errors will also get big-
ger. It is seen in Table (2) that approach 1 Root
Mean Square Error (RMSE) values are similar to
SMC for α = 0.1. Otherwise, the RMSE val-
ues decrease inversely proportional to the α value.
Figure 2. Θ 1 trajectory tracking under SMC and
FOSMC controllers The main reason for the positive effect of α is that
the derivative effect increases as α increases.
The angle control results of the 4 different
controllers for θ 1 and θ 2 are given in Figures (2, It is seen from the Figures (2, 3) that approach
3). For a fair comparison, all initial conditions, 2 has oscillation at α = 0.1 and α = 0.5. Ac-
and constants are chosen as the same. Only de- cording to Eq. (24) for α = 0 the approach 2
rivative values are changed. sliding surfaces is calculated based on the error
286