Page 58 - IJOCTA-15-3

S. Ahmed et.al. / IJOCTA, Vol.15, No.3, pp.426-434 (2025)
by Lemma 1:
2π π
T 2 = q µ µ µ = q µ
µ b b n − 4 2 1+ 4 2 1− 4 µ n − 4 b b
1 2 1 2
(28)
The total settling time can be calculated by in-
cluding T 1 and T 2 , validating the predefined-time
convergence of the proposed method in alignment
with the FoPtSMC scheme.

4. Simulation results
A simulation study evaluates the effectiveness
of the proposed FoPtSMC scheme applied to a
PUMA 3-DOF robotic manipulator with exter-
nal disturbances. The study describes the ma-
nipulator’s model parameters, and details of the
robot’s dynamics are taken from. 33 To validate
the performance of the proposed method, it has
been compared with a fractional-order finite-time
SMC scheme, 31 and the simulations have been
performed on the MATLAB/Simulink software.
The desired trajectories and uncertain dynamics
are provided as follows:

 
sin(tπ/3) − 1 + cos(tπ/5)
x d =  cos(tπ/5 + (π/2)) + sin(tπ/3)  ,
sin(tπ/5 + (π/2)) − 1
 
0.5 ˙x 1 + sin(3x 1 )
v u =  1.3 ˙x 2 − 1.8sin(2x 2 )  ,
−0.1 ˙x 3 − 0.5sin(x 3 )
 
0.5sin( ˙x 1 )
v d =  1.1sin( ˙x 2 )  .
0.15sin( ˙x 3 )
In addition, the appropriate parameters for the
developed FoPtSMC scheme are given in Table 1.

Table 1. Proposed control parameters
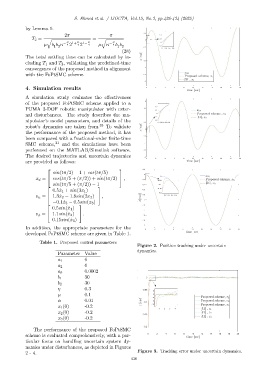
Figure 2. Position tracking under uncertain
dynamics.
Parameter Value
a 1 6
a 2 6
a 3 0.0002
b 1 30
b 2 30
η 0.3
µ 0.1
α 0.01
x 1 (0) -0.2
x 2 (0) -0.2
x 3 (0) -0.2

The performance of the proposed FoPtSMC
scheme is evaluated comprehensively, with a par-
ticular focus on handling uncertain system dy-
namics under disturbances, as depicted in Figures
Figure 3. Tracking error under uncertain dynamics.
2 - 4.
430