Page 214 - IJOCTA-15-4

H. Kravitz et al. / IJOCTA, Vol.15, No.4, pp.750-778 (2025)
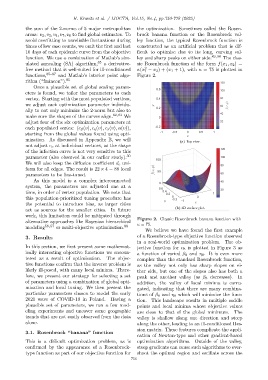
the sum of the 2-norms of 5 major metropolitan the optimization. Sometimes called the Rosen-
areas: v 2 , v 3 , v 4 , v 7 , v 8 to find global estimates. To brock banana function or the Rosenbrock val-
avoid overfitting to unreliable fluctuations during ley function, the typical Rosenbrock function is
times of low case counts, we omit the first and last constructed as an artificial problem that is dif-
10 days of each epidemic curve from the objective ficult to optimize due to its long, curving val-
function. We use a combination of Matlab’s sim- ley and sharp peaks on either side. 89,90 The clas-
ulated annealing (SA) algorithm, 85 a derivative- sic Rosenbrock function of the form f(x 1 , x 2 ) =
2
free method that is well-suited for ill-conditioned κ(x − x 2 ) + (x 1 + 1), with κ = 75 is plotted in
1
functions, 85–87 and Matlab’s interior point algo- Figure 2.
rithm (“fmincon”). 85
Once a plausible set of global scaling param-
eters is found, we tailor the parameters to each
vertex. Starting with the most populated vertices,
we adjust each optimization parameter individu-
ally to not only minimize the 2-norm but also to
make sure the shapes of the curves align. 62,63 We
adjust four of the six optimization parameters at
each populated vertex: (c β (v), c η (v), c λ (v), α(v)),
starting from the global values found using opti-
mization. As discussed in Appendix B, we will
not adjust c v at individual vertices, as the shape
of the infection curve is not very sensitive to this
parameter (also observed in our earlier study). 30
We will also keep the diffusion coefficient d e uni-
form for all edges. The result is 22 × 4 = 88 local
parameters to be fine-tuned.
As this model is a complex interconnected
system, the parameters are adjusted one at a
time, in order of vertex population. We note that
this population-prioritized tuning procedure has
the potential to introduce bias, as larger cities
act as sources for the smaller cities. In future
work, this limitation could be mitigated through
Figure 2. Classic Rosenbrock banana function with
alternative approaches like Bayesian hierarchical
modeling 56,57 or multi-objective optimization. 88 κ = 75.
We believe we have found the first example
3. Results of a Rosenbrock-type objective function observed
in a real-world optimization problem. The ob-
In this section, we first present some mathemat- jective function for v 8 is plotted in Figure 3 as
ically interesting objective functions we encoun- a function of varied β 8 and η 8 . It is even more
tered as a result of optimization. The objec- complex than the standard Rosenbrock function,
tive functions confirm that the inverse problem is as the valley not only has sharp slopes on ei-
likely ill-posed, with many local minima. There- ther side, but one of the slopes also has both a
fore, we present our strategy for selecting a set peak and another valley (as β 8 decreases). In
of parameters using a combination of global opti- addition, the valley of local minima is corru-
mization and local tuning. We then present the gated, indicating that there are many combina-
particular parameters chosen to model the early tions of β 8 and η 8 which will minimize the func-
2021 wave of COVID-19 in Poland. Having a tion. This landscape results in multiple saddle
plausible set of parameters, we run a few mod- points and local minima whose objective values
eling experiments and uncover some geographic are close to that of the global minimum. The
trends that are not easily observed from the data valley is shallow along one direction and steep
alone. along the other, leading to an ill-conditioned Hes-
sian matrix. These features complicate the appli-
3.1. Rosenbrock “banana” function
cation of Newton-type and other gradient-based
This is a difficult optimization problem, as is optimization algorithms. Outside of the valley,
confirmed by the appearance of a Rosenbrock- steep gradients can cause such algorithms to over-
type function as part of our objective function for shoot the optimal region and oscillate across the
756