Page 117 - MSAM-3-2

Materials Science in Additive Manufacturing Hybrid lattice structures design with AI

about 20 min to calculate the elastic modulus and Poisson’s 2.4. Homogenization method
ratio of a lattice running on six cores Intel I7-8700K CPU The elastic modulus and Poisson’s ratio of the hybrid lattice
®
at 3.7 GHz. were calculated based on the homogenization method.
According to homogenization theory, the elasticity tensor
A B of a periodic structure can be determined by:
1 ij ij ij ij
E ijkl ' E pqrs 0 pq pq rs 0 rs d (XI)
H

where E is the locally varying stiffness tensor, |Ω| is
pqrs
ij
the area of the domain, 0 refers to the applied strain
pq
fields at the macroscopic scale, and pq ij refers to the locally
C D
varying strain fields given by:
χ
ij
ε ( ) ij ε = pq ( ) ( χ= 1 2 ij , p q χ + ij , q p ) (XII)
pq
χ is the displacement field that can be determined
ij
based on applied macroscopic strain:
kl
d

E kl E 0 dV
ijpq ij pq ijpq ij pq

(XIII)
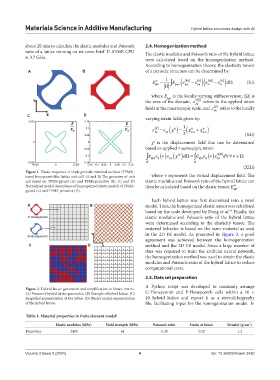
Figure 1. Elastic responses of triply periodic minimal surfaces (TPMS)-
based honeycomb-like lattice unit cell. (A and B) The geometry of unit where ν represents the virtual displacement field. The
cell based on TPMS-gyroid (A) and TPMS-primitive (B). (C and D) elastic modulus and Poisson’s ratio of the hybrid lattice can
H
Normalized spatial dependence of homogenized elastic moduli of TPMS- then be calculated based on the elastic tensor E .
gyroid (C) and TPMS-primitive (D). ijkl
Each hybrid lattice was first discretized into a voxel
A B model. Then, the homogenized elastic tensor was calculated
based on the code developed by Dong et al. Finally, the
54
elastic modulus and Poisson’s ratio of the hybrid lattice
were determined according to the elasticity tensor. The
material behavior is based on the same material as used
in the 2D FE model. As presented in Figure 3, a good
agreement was achieved between the homogenization
C D method and the 2D FE model. Since a large number of
data was required to train the artificial neural network,
the homogenization method was used to obtain the elastic
modulus and Poisson’s ratio of the hybrid lattice to reduce
computational costs.

2.5. Data set preparation
A Python script was developed to randomly arrange
Figure 2. Hybrid lattice generation and simplification to binary matrix.
(A) Process of hybrid lattice generation. (B) Example of hybrid lattice. (C) G-Honeycomb and P-Honeycomb cells within a 10 ×
Simplified representation of the lattice. (D) Binary matrix representation 10 hybrid lattice and export it as a stereolithography
of the hybrid lattice. file, facilitating input for the homogenization model. In

Table 1. Material properties in finite element model

3
Elastic modulus (MPa) Yield strength (MPa) Poisson’s ratio Strain at break Density (g/cm )
Properties 2400 61 0.35 0.25 1.2

Volume 3 Issue 2 (2024) 4 doi: 10.36922/msam.3430