Page 124 - IJOCTA-15-2

Parallel late acceptance hill-climbing for binary-encoded optimization problems
Table 5. Gap scores on UFLP instances for different values of L on using 16 threads

Instance L=10 L=20 L=50 L=100
cap71 0.00 0.00 0.00 0.00
cap72 0.00 0.00 0.00 0.00
cap73 0.00 0.00 0.00 0.00
cap74 0.00 0.00 0.00 0.00
cap101 0.00 0.00 0.00 0.00
cap102 0.00 0.00 0.00 0.00
cap103 0.01 0.00 0.00 0.00
cap104 0.00 0.00 0.00 0.00
cap131 0.16 0.08 0.00 0.04
cap132 0.03 0.00 0.00 0.01
cap133 0.01 0.03 0.05 0.03
cap134 0.00 0.00 0.00 0.00
capa 2.72 1.97 5.73 53.26
capb 2.20 1.57 2.77 20.47
capc 1.66 1.38 2.03 15.10
Avg.Gap 0.45 0.34 0.71 5.93

Table 6. Gap scores on UFLP instances for different values of L on using 32 threads

Instance L=10 L=20 L=50 L=100
cap71 0.00 0.00 0.00 0.00
cap72 0.00 0.00 0.00 0.00
cap73 0.00 0.00 0.00 0.00
cap74 0.00 0.00 0.00 0.00
cap101 0.00 0.00 0.00 0.00
cap102 0.00 0.00 0.00 0.00
cap103 0.00 0.00 0.00 0.00
cap104 0.00 0.00 0.00 0.00
cap131 0.02 0.06 0.05 1.22
cap132 0.00 0.00 0.01 1.54
cap133 0.00 0.00 0.04 0.75
cap134 0.00 0.00 0.00 2.98
capa 1.76 1.90 52.37 103.31
capb 1.58 1.63 21.14 42.93
capc 1.43 1.36 14.85 31.94
Avg.Gap 0.32 0.33 5.90 12.31
12.00
10.00

9.00
6.96
Speedup 6.00 5.52

3.00 3.33

0.00
4 8 16 32
Number of Threads

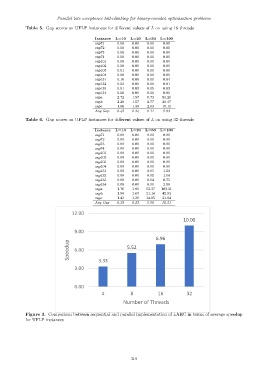
Figure 3. Comparison between sequential and parallel implementation of LAHC in terms of average speedup
for UFLP instances

319