Page 125 - IJOCTA-15-2

¨
E. Sonu¸c, E. Ozcan / IJOCTA, Vol.15, No.2, pp.311-329 (2025)
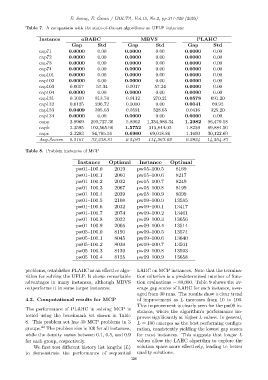
Table 7. A comparison with the state-of-the-art algorithms on UFLP instances

Instance oBABC MBVS PLAHC
Gap Std Gap Std Gap Std
cap71 0.0000 0.00 0.0000 0.00 0.0000 0.00
cap72 0.0000 0.00 0.0000 0.00 0.0000 0.00
cap73 0.0000 0.00 0.0000 0.00 0.0000 0.00
cap74 0.0000 0.00 0.0000 0.00 0.0000 0.00
cap101 0.0000 0.00 0.0000 0.00 0.0000 0.00
cap102 0.0000 0.00 0.0000 0.00 0.0000 0.00
cap103 0.0017 57.34 0.0017 57.34 0.0000 0.00
cap104 0.0000 0.00 0.0000 0.00 0.0000 0.00
cap131 0.1010 813.74 0.0112 270.21 0.0578 691.20
cap132 0.0125 236.72 0.0000 0.00 0.0041 69.92
cap133 0.0409 395.63 0.0591 328.65 0.0416 325.20
cap134 0.0000 0.00 0.0000 0.00 0.0000 0.00
capa 2.8969 299,727.30 5.8962 1,334,986.34 1.2982 96,479.58
capb 2.3595 102,565.90 1.5752 313,844.03 1.8239 89,884.50
capc 2.3283 94,785.55 0.6960 69,018.86 1.1600 30,122.69
Avg.Scores 0.5161 33,238.81 0.5493 114,567.02 0.2924 14,504.87

Table 8. Problem instances of MCP

Instance Optimal Instance Optimal
pw01–100.0 2019 pw05–100.5 8169
pw01–100.1 2060 pw05–100.6 8217
pw01–100.2 2032 pw05–100.7 8249
pw01–100.3 2067 pw05–100.8 8199
pw01–100.4 2039 pw05–100.9 8099
pw01–100.5 2108 pw09–100.0 13585
pw01–100.6 2032 pw09–100.1 13417
pw01–100.7 2074 pw09–100.2 13461
pw01–100.8 2022 pw09–100.3 13656
pw01–100.9 2005 pw09–100.4 13514
pw05–100.0 8190 pw09–100.5 13574
pw05–100.1 8045 pw09–100.6 13640
pw05–100.2 8039 pw09–100.7 13501
pw05–100.3 8139 pw09–100.8 13593
pw05–100.4 8125 pw09–100.9 13658

problems, establishes PLAHC as an effective algo- LAHC on MCP instances. Note that the termina-
rithm for solving the UFLP. It shows remarkable tion criterion is a predetermined number of func-
advantages in many instances, although MBVS tion evaluations = 80,000. Table 9 shows the av-
outperforms it in some larger instances. erage gap scores of LAHC for each instance, aver-
aged from 30 runs. The results show a clear trend
4.2. Computational results for MCP of improvement as L increases from 10 to 100.
This improvement is clearly seen for the pw09 in-
The performance of PLAHC in solving MCP is
stances, where the algorithm’s performance im-
tested using the benchmark set shown in Table proves significantly at higher L values. In general,
8. This problem set has 30 MCP problems in 3 L = 100 emerges as the best performing configu-
groups. 42 The problem size is 100 for all instances, ration, consistently yielding the lowest gap scores
while the density varies between 0.1, 0.5, and 0.9 for most instances. This suggests that longer L
for each group, respectively. values allow the LAHC algorithm to explore the
We first test different history list lengths (L) solution space more effectively, leading to better
to demonstrate the performance of sequential quality solutions.
320