Page 64 - IJOCTA-15-2

Multiple item economic lot sizing problem with inventory dependent demand
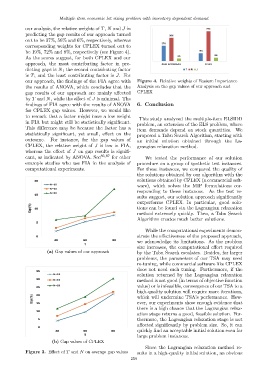
our analysis, the relative weights of T, N and J in
predicting the gap results of our approach turned
out to be 37%, 56% and 6%, respectively, whereas
corresponding weights for CPLEX turned out to
be 19%, 72% and 8%, respectively (see Figure 4).
As the scores suggest, for both CPLEX and our
approach, the most contributing factor in pre-
dicting gaps is N; the second contributing factor
is T; and the least contributing factor is J. For
our approach, the findings of the FIA agree with Figure 4. Relative weights of Feature Importance
the results of ANOVA, which concludes that the Analysis on the gap values of our approach and
gap results of our approach are mainly affected CPLEX
by T and N, while the effect of J is minimal. The
findings of FIA agree with the results of ANOVA 6. Conclusion
for CPLEX gap values. However, we would like
to remark that a factor might have a low weight
This study analyzed the multiple-item ELSIDD
in FIA but might still be statistically significant. problem, an extension of the ELS problem, where
This difference may be because the factor has a
item demands depend on stock quantities. We
statistically significant, yet small, effect on the proposed a Tabu Search Algorithm, starting with
outcome. For instance, for the gap values of an initial solution obtained through the La-
CPLEX, the relative weight of J is low in FIA, grangian relaxation method.
whereas the effect of J on gap results is signifi-
cant, as indicated by ANOVA. See 86,87 for other We tested the performance of our solution
example studies who use FIA in the analysis of procedure on a group of synthetic test instances.
computational experiments. For these instances, we compared the quality of
the solutions obtained by our algorithm with the
solutions obtained by CPLEX (a commercial soft-
ware), which solves the MIP formulations cor-
responding to these instances. As the test re-
sults suggest, our solution approach significantly
outperforms CPLEX. In particular, good solu-
tions can be found via the Lagrangian relaxation
method extremely quickly. Then, a Tabu Search
Algorithm creates much better solutions.

While the computational experiments demon-
strate the effectiveness of the proposed approach,
we acknowledge its limitations. As the problem
size increases, the computational effort required
(a) Gap values of our approach by the Tabu Search escalates. Besides, for larger
problems, the parameters of our TSA may need
re-tuning, while commercial software like CPLEX
does not need such tuning. Furthermore, if the
solution returned by the Lagrangian relaxation
method is not good (in terms of objective function
value) or is infeasible, convergence of our TSA to a
high-quality solution will require more iterations,
which will undermine TSA’s performance. How-
ever, our experiments show enough evidence that
there is a high chance that the Lagrangian relax-
ation stage returns a good, feasible solution. Fur-
thermore, the Lagrangian relaxation stage is not
affected significantly by problem size. So, it can
quickly find an acceptable initial solution even for
large problem instances.
(b) Gap values of CPLEX
Since the Lagrangian relaxation method re-
Figure 3. Effect of T and N on average gap values sults in a high-quality initial solution, an obvious
259