Page 12 - IJOCTA-15-3

A. Kaveh, M. Vahedi, M. Gandomkar / IJOCTA, Vol.15, No.3, pp.379-395 (2025)
By solving Equations (2.1)–(11), three fixed Which always holds for σ > 2. Therefore, the
points are obtained. We derive these equilibrium eigenvalues would be:
points and discuss their local behavior.

2.2. Bifurcation and chaos in the 2 2σ(σ+1) (16)
brushless direct current system ω = σ−2 > 0
Hopf bifurcation occurs when the correspond-
Therefore, the eigenvalues will be as follows:
ing Jacobian matrix has a pair of pure imag-
inary poles and other eigenvalues of the real
part are non-zero. Here, for the BLDC sys- r
tem, the Hopf bifurcation and its chaotic be- λ 1 = −(σ + 2), λ 2,3 = ±j 2σ(σ + 1) (17)
havior under no-load condition ( u = u q = σ − 2
d
T L = 0 ) are investigated.
g By examining
Equations (2.1)–Equation (11), it is clear that Therefore, γ = γ h corresponds to a Hopf bi-
E 1 = (0, 0, 0) is the first equilibrium point. furcation point of the system and for values close
And with γ > 1, two other nontrivial equilib- to γ ̸= γ h , the equilibria are surrounded by
√
√
ria are E 2 = ( γ −1, γ−1, γ−1) and the limit cycle, and for γ > γ h , all three equi-
√
√
E 3 = ( γ −1, − γ−1, − γ−1). A simple libria would be unstable. System (8) does not
analysis shows that if 0 < γ < 1, the original change under (x, y, z) ⇔ (x, −y, −z); thus, it can
equilibrium point is stable, and it loses its stabil- be said that it is symmetric regarding the y and z
∂
∂
∂

ity for γ = 1 and creates two unreal equilibrium axes, and if ∇V = ∂x dx + ∂y dx + ∂z dx =
dt
dt
dt
points that are initially stable. By linearizing the −(σ + 2) < 0, this system is convergent.
system, we obtain the Jacobian matrix to discuss As mentioned before, if γ ≤ 1, E 1 = (0, 0, 0)
the local behavior of its equilibrium points. The is the only equilibrium point. When the system
Jacobian matrix of the system is as follows 26 : parameters change, we might expect BLDC to
demonstrate stable, limited cycle, and chaotic be-
 
−1 x 3 x 2 haviors.
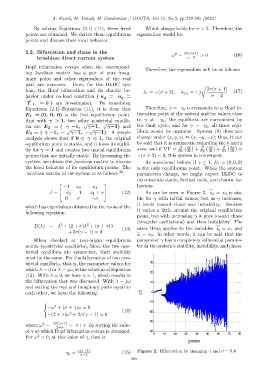
J = −x 3 −1 −x 1 + γ  (12) As can be seen in Figure 2, i d = x 2 is sta-
f

0 σ −σ ble for γ with initial values, but as γ increases,
it tends toward chaos and instability. Because
which has eigenvalues obtained by the roots of the
it varies a little around the original equilibrium
following equation:
point, but with increasing γ it goes toward chaos
(irregular oscillations) and then instability. The
3
2
D(λ) = λ + (2 + σ)λ + (σ + γ)λ
(13) same thing applies to the variables i q = x 1 and
f
+2σ(γ − 1) = 0
e ω = x 3 . In other words, it can be said that the
When checked at non-origin equilibrium parameter γ has a completely influential parame-
points (nontrivial equilibria), Since the two non- ter in the system’s stability, instability, and chaos.
trivial equilibria are symmetric, their stability
must be the same. For the bifurcation of two non-
trivial equilibria, that is, the parameter values for
which λ = 0 or λ = jω, is the solution of Equation
(13). With λ = 0, we have γ = 1, which results in
the bifurcation that was discussed. With λ = jω
and setting the real and imaginary parts equal to
each other, we have the following:
(
3
−ω + (σ + γ)ω = 0
(14)
2
−(2 + σ)ω + 2σ(γ − 1) = 0
2
where ω = 2σ(γ−1) = σ+γ. By sorting the value
2+σ
of γ at which Hopf bifurcation occurs is obtained.
2
For ω > 0, at this value of γ, that is:
σ(σ+4) Figure 2. Bifurcation by changing γ and σ = 5.4
γ h = (15)
σ−2
384