Page 13 - IJOCTA-15-3

Improving the performance of a chaotic nonlinear system of fractional-order...
3. Control strategy for chaos Furthermore, Figures 4 and 5 present the
suppression chaotic state trajectories of the FO-BLDC sys-
tem without a control signal.
This study considers the following assumptions to
ensure the accurate modeling and practical fea-
sibility of the proposed FO-SMC for the BLDC
system.

s

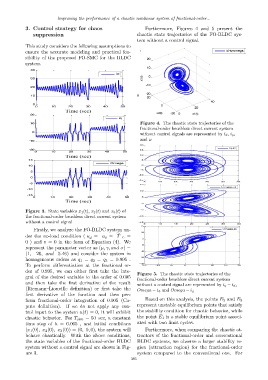
Figure 4. The chaotic state trajectories of the
fractional-order brushless direct current system
without control signals are represented by i d , i q ,
and ω

Figure 3. State variables x 1 (t), x 2 (t) and x 3 (t) of
the fractional-order brushless direct current system
without a control signal
Firstly, we analyze the FO-BLDC system un-
der the no-load condition ( u = u q = T L =
f
d
0 ) and v = 0 in the form of Equation (4). We
represent the parameter vector as (µ, γ, and σ) =
(1, 20, and 5.46) and consider the system in
homogeneous orders as q 1 = q 2 = q 3 = 0.995 .
To perform differentiation at the fractional or-
der of 0.995, we can either first take the inte-
Figure 5. The chaotic state trajectories of the
gral of the desired variable to the order of 0.005
fractional-order brushless direct current system
and then take the first derivative of the result without a control signal are represented by i q − i d ,
(Riemann–Liouville definition) or first take the
Omega − i d and Omega − i q
first derivative of the function and then per-
form fractional-order integration of 0.005 (Ca- Based on this analysis, the points E 2 and E 3
puto definition). If we do not apply any con- represent unstable equilibrium points that satisfy
trol input to the system u(t) = 0, it will exhibit the stability condition for chaotic behavior, while
chaotic behavior. For T sim = 50 sec, a constant the point E 1 is a stable equilibrium point associ-
time step of h = 0.005 , and initial conditions ated with two limit cycles.
(x 1 (0), x 2 (0), x 3 (0)) = (0, 0, 0), the system will Furthermore, when comparing the chaotic at-
behave chaotically. With the above conditions, tractors of the fractional-order and conventional
the state variables of the fractional-order BLDC BLDC systems, we observe a larger stability re-
system without a control signal are shown in Fig- gion (attraction region) for the fractional-order
ure 3. system compared to the conventional one. For
385