Page 98 - IJOCTA-15-3

Sayed Saber et.al. / IJOCTA, Vol.15, No.3, pp.464-482 (2025)
Table 4. Approximation errors for JSCSM and MSGDTM at different truncation orders

Truncation Order (N) Error (JSCSM) Error (MSGDTM)
5 3.21 × 10 −2 2.11 × 10 −2
10 1.47 × 10 −2 8.95 × 10 −3
15 7.63 × 10 −3 4.02 × 10 −3

Relative Error of MSGDTM vs JSCSM Absolute Error of MSGDTM vs JSCSM
15 0.045
Glucose (x) Glucose (x)
Insulin (y) 0.04 Insulin (y)
Beta Cells (z) Beta Cells (z)
0.035
10 0.03
Relative Error Absolute Error 0.025
0.02
5 0.015
0.01
0.005
0 0
0 1 2 3 4 5 6 0 1 2 3 4 5 6
Time Time
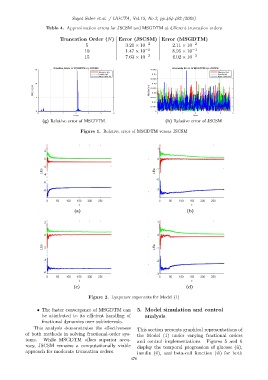
(g) Relative error of MSGDTM. (h) Relative error of JSCSM
Figure 1. Relative error of MSGDTM versus JSCSM

(a) (b)

(c) (d)

Figure 2. Lyapunov exponents for Model (1)

• The faster convergence of MSGDTM can 5. Model simulation and control
be attributed to its efficient handling of analysis
fractional dynamics over subintervals.
This analysis demonstrates the effectiveness This section presents graphical representations of
of both methods in solving fractional-order sys- the Model (1) under varying fractional orders
tems. While MSGDTM offers superior accu- and control implementations. Figures 5 and 6
racy, JSCSM remains a computationally viable display the temporal progression of glucose (ˆu),
approach for moderate truncation orders. insulin (ˆv), and beta-cell function ( ˆw) for both
470