Page 124 - IJOCTA-15-4

Zhang et al. / IJOCTA, Vol.15, No.4, pp.649-669 (2025)
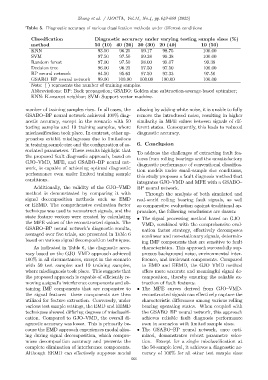
Table 5. Diagnostic accuracy of various classification methods under different conditions

Classification Diagnostic accuracy under varying testing sample sizes (%)
method 50 (10) 40 (20) 30 (30) 20 (40) 10 (50)
KNN 93.50 96.25 99.17 98.75 100.00
SVM 97.50 97.50 99.38 99.38 100.00
Random forest 97.00 97.50 98.00 99.07 99.38
Decision tree 96.00 96.25 97.50 97.50 100.00
BP neural network 84.50 95.63 97.50 97.33 97.50
GSABO–BP neural network 99.00 100.00 100.00 100.00 100.00
Note: ( ) represents the number of training samples.
Abbreviations: BP: Back propagation; GSABO: Golden sine subtraction-average-based optimizer;
KNN: K-nearest neighbor; SVM: Support vector machine.

number of training samples rises. In all cases, the aliasing by adding white noise, it is unable to fully
GSABO–BP neural network achieved 100% diag- remove the introduced noise, resulting in higher
nostic accuracy, except in the scenario with 50 similarity in MFE values between signals of dif-
testing samples and 10 training samples, where ferent states. Consequently, this leads to reduced
misclassification took place. In contrast, other ap- diagnostic accuracy.
proaches exhibit misdiagnoses due to limitations
in training sample size and the configuration of as- 6. Conclusion
sociated parameters. These results highlight that To address the challenges of extracting fault fea-
the proposed fault diagnostic approach, based on tures from rolling bearings and the unsatisfactory
GJO–VMD, MFE, and GSABO–BP neural net- diagnostic performance of conventional classifica-
work, is capable of achieving optimal diagnostic tion models under small-sample size conditions,
performance even under limited training sample
this study proposes a fault diagnosis method that
conditions.
integrates GJO–VMD and MFE with a GSABO–
Additionally, the validity of the GJO–VMD BP neural network.
method is demonstrated by comparing it with Through the analysis of both simulated and
signal decomposition methods such as EMD real-world rolling bearing fault signals, as well
or EEMD. The comprehensive evaluation factor as comparative evaluation against traditional ap-
technique was used to reconstruct signals, and the proaches, the following conclusions are drawn:
state feature vectors were created by calculating
• The signal processing method based on GJO–
the MFE values of the reconstructed signals. The
VMD, combined with the comprehensive eval-
GSABO–BP neural network’s diagnostic results,
uation factor strategy, effectively decomposes
averaged over five trials, are presented in Table 6
nonlinear and non-stationary signals, determin-
based on various signal decomposition techniques.
ing IMF components that are sensitive to fault
As indicated in Table 6, the diagnostic accu- characteristics. This approach successfully sup-
racy based on the GJO–VMD approach achieved presses background noise, environmental inter-
100% in all circumstances, except in the scenario ference, and irrelevant components. Compared
with 50 test samples and 10 training samples, to EMD and EEMD, the GJO–VMD method
where misdiagnosis took place. This suggests that offers more accurate and meaningful signal de-
the proposed approach is capable of efficiently re- composition, thereby ensuring the reliable ex-
moving a signal’s interference components and ob- traction of fault features.
taining IMF components that are responsive to • The MFE curves derived from GJO–VMD-
the signal features—these components are then reconstructed signals can effectively capture the
utilized for feature extraction. Conversely, under characteristic differences among various rolling
various test sample settings, the EMD and EEMD bearing operating states. When coupled with
techniques showed differing degrees of misclassifi- the GSABO–BP neural network, this approach
cation. Compared to GJO–VMD, the overall di- achieves reliable fault diagnosis performance
agnostic accuracy was lower. This is primarily be- even in scenarios with limited sample sizes.
cause the EMD approach experiences modal alias- • The GSABO–BP neural network, once opti-
ing during signal decomposition, which compro- mized, demonstrates robust parameter selec-
mises decomposition accuracy and prevents the tion. Except for a single misclassification at
complete elimination of interference components. the 50-sample level, it achieves a diagnostic ac-
Although EEMD can effectively suppress modal curacy of 100% for all other test sample sizes
666