Page 177 - IJOCTA-15-4

African vultures optimization-based hybrid neural network–proportional-integral-derivative controller...

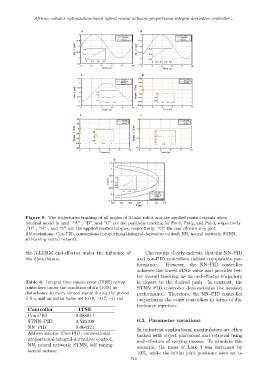
Figure 9. The trajectories tracking of all angles of 3-links robot and the applied control signals when
nominal model is used. “A” , “B”, and “C” are the positions tracking for Psi-1, Psi-2, and Psi-3, respectively
.”D” , “E” , and “F” are the applied control torques, respectively. “G” the end effector x–y plot.
Abbreviations: Con-PID, conventional proportional-integral-derivative control; NN, neural network; STNN,
self-tuning neural network.

the 3-LRRM end-effector under the influence of The results clearly indicate that the NN–PID
the disturbance. and con-PID controllers deliver comparable per-
formance. However, the NN–PID controller
achieves the lowest ITSE value and provides bet-
ter overall tracking, as its end-effector trajectory
Table 6. Integral time square error (ITSE) across is closest to the desired path. In contrast, the
controllers under the condition of sin (100t) as STNN–PID controller demonstrates the weakest
disturbance to every control signal during the period performance. Therefore, the NN–PID controller
2–6 s, and an initial value set to (0, −0.7, −1) rad outperforms the other controllers in terms of dis-
turbance rejection.
Controller ITSE
Con-PID 0.088811
STNN–PID 3.526199 6.3. Parameter variations
NN–PID 0.064321
In industrial applications, manipulators are often
Abbreviations: Con-PID, conventional
tasked with object placement and retrieval using
proportional-integral-derivative control;
end effectors of varying masses. To simulate this
NN, neural network; STNN, self-tuning
scenario, the mass of Link 3 was increased by
neural networ.
10%, while the initial joint positions were set to
719