Page 229 - IJOCTA-15-4

Data-driven optimization and parameter estimation for an epidemic model
Table 3. Populated vertices along with their initial conditions and parameter values. The skipping parameter
v
v is scaled by c v = 0.306 at all vertices, including the unpopulated ones, while the diffusion coefficient is kept
constant for all edges at d e = 0.09.
c
Vertex S(0) I(0) β · S(0) η α λ
1 - Pozna´n 454,442 670 0.41 0.33 0.88 0.08
2 - Wroc law 571,100 504 0.43 0.34 0.88 0.05
3 - Katowice, Sosnowiec, Zabrze, & Bytom 704,112 570 0.43 0.34 0.95 0.05
4 - Krak´ow 701,725 470 0.44 0.34 0.88 0.05
5 - Rzesz´ow 186,080 230 0.46 0.36 0.55 0.05
6 - Radom 186,894 124 0.44 0.34 0.80 0.05
7 - L´od´z 581,453 600 0.44 0.36 0.60 0.06
8 - Warszawa (Warsaw) 1,610,924 1,941 0.45 0.36 0.886 0.05
9 - Gda´nsk & Gdynia 629,924 1,204 0.46 0.39 0.65 0.05
10 - Bielsko-Bia la 152,621 123 0.41 0.31 0.88 0.05
11 - Lublin 308,636 331 0.45 0.39 0.88 0.05
12 - Bia lystok 264,085 367 0.45 0.39 0.88 0.05
13 - Szczecin 339,467 435 0.46 0.38 0.70 0.10
14 - Kielce 175,855 152 0.42 0.32 0.88 0.05
15 - Czestochowa 193,876 149 0.45 0.36 0.88 0.05
16 - Bydgoszcz 291,460 613 0.41 0.35 0.80 0.08
17 - Suwa lki 65,475 51 0.46 0.38 0.88 0.05
18 - Zielona G´ora 127,869 216 0.50 0.43 0.88 0.05
19 - Gorz´ow Wielkopolski 106,383 196 0.51 0.43 0.88 0.05
20 - Rybnik 122,801 62 0.42 0.33 0.88 0.05
´
21 - Swinouj´scie 35,295 54 0.50 0.41 0.88 0.05
22 - Toru´n 171,744 374 0.44 0.39 0.88 0.06

v
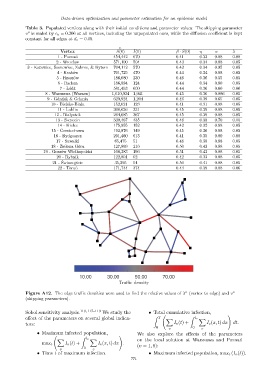
Figure A12. The edge traffic densities were used to find the relative values of λ (vertex to edge) and v v
(skipping parameters).

Sobol sensitivity analysis. 110,117–119 We study the • Total cumulative infection,
!
effect of the parameters on several global indica- Z T X Z l e X
I v (t) + I e (x, t) dx dt.
tors:
0 v 0 e
• Maximum infected population, We also explore the effects of the parameters
!
Z
X l e X on the local solution at Warszawa and Pozna´n
max t I v (t) + I e (x, t) dx . (v = 1, 8):
v 0 e
• Time t of maximum infection. • Maximum infected population, max t (I v (t)).
771