Page 56 - IJB-6-2

Effects of topology optimization in multimaterial 3D bioprinting of soft actuators
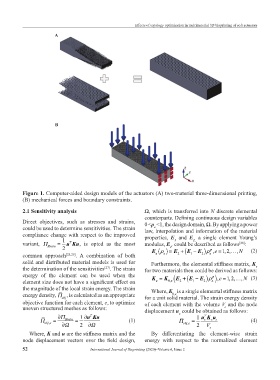
A

B

Figure 1. Computer-aided design models of the actuators (A) two-material three-dimensional printing,
(B) mechanical forces and boundary constraints.

2.1 Sensitivity analysis Ω, which is transferred into N discrete elemental
counterparts. Defining continuous design variables
Direct objectives, such as stresses and strains, 0 <ρ <1, the design domain, Ω. By applying a power
could be used to determine sensitivities. The strain law, interpolation and information of the material
e
compliance change with respect to the improved properties, E and E a single element Young’s
1
2,
variant,  = 1 uKu, is opted as the most modulus, E , could be described as follows :
T
[28]
Strain
2 E  e E +( E − ) p ,e =12, , …, N (2)
E  ( ) =
common approach [25,26] . A combination of both e e 2 1 2 e
solid and distributed material models is used for Furthermore, the elemental stiffness matrix, K
the determination of the sensitivities . The strain for two materials then could be derived as follows: e
[27]
energy of the element can be used when the K = K ( E +( E − ) ), p e …, N (3)
E
element size does not have a significant effect on e 0, e 2 1 2 e =12, ,
the magnitude of the local strain energy. The strain Where, K is a single elemental stiffness matrix
energy density,  , is calculated as an appropriate for a unit solid material. The strain energy density
0,e
obj
objective function for each element, e, to optimize of each element with the volume V and the node
uneven structured meshes as follows: displacement u could be obtained as follows:
e
T
∂  1 ∂u Ku e 1 uK u
T
 = Strain = (1)  = e ee (4)
∂ obj ,e  2 ∂  obj e, 2 V e
Where, K and u are the stiffness matrix and the By differentiating the element-wise strain
node displacement vectors over the field design, energy with respect to the normalized element
52 International Journal of Bioprinting (2020)–Volume 6, Issue 2