Page 331 - v11i4

International Journal of Bioprinting Nozzle geometry for enhanced cell viability

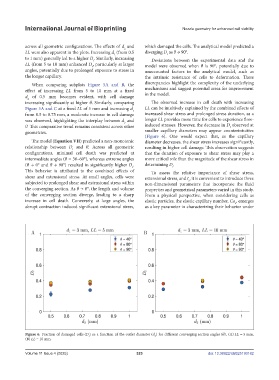
across all geometric configurations. The effects of d and which damaged the cells. The analytical model predicted a
2
LL were also apparent in the plots. Increasing d (from 0.5 diverging D as θ → 90°.
t
2
to 1 mm) generally led to a higher D . Similarly, increasing Deviations between the experimental data and the
t
LL (from 5 to 10 mm) enhanced D , particularly at larger model were observed when θ is 90°, potentially due to
t
angles, potentially due to prolonged exposure to stress in unaccounted factors in the analytical model, such as
the longer capillary. the intrinsic resistance of cells to deformation. These
When comparing subplots Figure 5A and B, the discrepancies highlight the complexity of the underlying
effect of increasing LL from 5 to 10 mm at a fixed mechanisms and suggest potential areas for improvement
d of 0.5 mm becomes evident, with cell damage in the model.
2
increasing significantly at higher θ. Similarly, comparing The observed increase in cell death with increasing
Figure 5A and C at a fixed LL of 5 mm and increasing d LL can be intuitively explained by the combined effects of
2
from 0.5 to 0.75 mm, a moderate increase in cell damage increased shear stress and prolonged stress duration, as a
was observed, highlighting the interplay between d and longer LL provides more time for cells to experience flow-
2
θ. This comparative trend remains consistent across other induced stresses. However, the decrease in D observed at
t
geometries. smaller capillary diameters may appear counterintuitive
(Figure 6). One would expect that, as the capillary
The model (Equation VII) predicted a non-monotonic diameter decreases, the shear stress increases significantly,
relationship between D and θ. Across all geometric resulting in higher cell damage. This observation suggests
t
configurations, minimal cell death was predicted at that the duration of exposure to shear stress may play a
intermediate angles (θ ≈ 30–60°), whereas extreme angles more critical role than the magnitude of the shear stress in
(θ → 0° and θ → 90°) resulted in significantly higher D . determining D . t
t
This behavior is attributed to the combined effects of To assess the relative importance of shear stress,
shear and extensional stress. At small angles, cells were extensional stress, and t , it is convenient to introduce three
s
subjected to prolonged shear and extensional stress within non-dimensional parameters that incorporate the fluid
the converging section. As θ → 0°, the length and volume properties and geometrical parameters varied in this study.
of the converging section diverge, leading to a sharp From a physical perspective, when considering cells as
increase in cell death. Conversely, at large angles, the elastic particles, the elastic capillary number, Ca , emerges
e
abrupt contraction induced significant extensional stress, as a key parameter in characterizing their behavior under

Figure 6. Fraction of damaged cells (D ) as a function of the outlet diameter (d ) for different converging section angles (θ). (A) LL = 5 mm.
t
2
(B) LL = 10 mm.
Volume 11 Issue 4 (2025) 323 doi: 10.36922/IJB025190182