Page 16 - IJOCTA-15-1

P. Kumar / IJOCTA, Vol.15, No.1, pp.1-13 (2025)

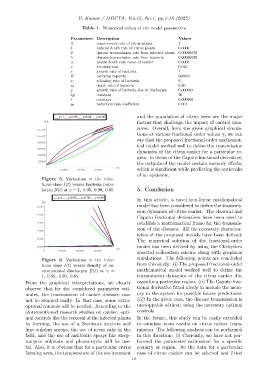
Table 1. Numerical values of the model parameters

Parameters Description Values
Λ requirement rate of citrus plants 2
δ natural death rate of citrus plants 0.0006
β disease transmission rate from infected plants 0.00000035
λ disease transmission rate from bacteria 0.00000035
α plants death rate cause of canker 0.0008
ν recovery rate 0.015
s growth rate of bacteria 1
K carrying capacity 500000
s 1 releasing rate of bacteria 8
s 0 death rate of bacteria 0.60
g growth rate of bacteria due to discharges 0.000003
Q 0 constant 20
l constant 0.000006
g 0 reduction rate coefficient 0.001

___γ=1,___γ=0.95,___γ=0.90,___γ=0.85 and the population of citrus trees are the major
B(t) factors that challenge the impact of control mea-
sures. Overall, from the given graphical simula-
1.2 × 10 6
tions at various fractional order values γ, we can
1.0 × 10 6
say that the proposed fractional-order mathemat-
800000
ical model worked well to define the transmission
600000
dynamics of the citrus canker for a particular re-
400000
gion. In terms of the Caputo fractional derivative,
200000
the outputs of the model contain memory effects,
I(t)
100000 200000 300000 which is significant while predicting the outbreaks
of an epidemic.
Figure 5. Variations in the infec-
tious class I(t) versus bacteria popu-
lation B(t) at γ = 1, 0.95, 0.90, 0.85. 5. Conclusion
___γ=1,___γ=0.95,___γ=0.90,___γ=0.85
E(t) In this article, a novel non-linear mathematical
12500 model has been considered to define the transmis-
sion dynamics of citrus canker. The classical and
12000
Caputo fractional derivatives have been used to
11500 establish a mathematical frame for the transmis-
sion of the diseases. All the necessary character-
11000
istics of the proposed models have been defined.
10500
The numerical solution of the fractional-order
10000 model has been derived by using the Chebyshev
I(t)
0 100000 200000 300000
spectral collocation scheme along with graphical
simulations. The following points are concluded
Figure 6. Variations in the infec-
tious class I(t) versus density of en- from this study: (i) The proposed fractional-order
vironmental discharges E(t) at γ = mathematical model worked well to define the
1, 0.95, 0.90, 0.85. transmission dynamics of the citrus canker dis-
From the graphical interpretations, we clearly eases for a particular region. (ii) The Caputo frac-
observe that for the considered parameter esti- tional derivative fitted nicely to include the mem-
mates, the transmission of canker diseases can- ory in the system for possible future predictions.
not be stopped easily. In that case, some extra- (iii) In the given case, the disease transmission is
optimal controls will be needed. According to the unstoppable without using the necessary optimal
aforementioned research studies on canker, opti- controls.
mal controls like the removal of the infected plants In the future, this study can be easily extended
by burning, the use of a Bordeaux mixture and to simulate more results on citrus canker trans-
lime sulphur sprays, the use of neem cake in the mission. The following analysis can be performed
field, and the use of antibiotic sprays like strep- in this direction: (i) Currently, we have not per-
tomycin sulphate and phonomycin will be use- formed the parameter estimation for a specific
ful. Also, it is obvious that for a particular citrus country or region. So the data for a particular
farming area, the temperature of the environment case of citrus canker can be selected and fitted
10