Page 148 - IJOCTA-15-3
P. 148
E.M. Shaban / IJOCTA, Vol.15, No.3, pp.517-534 (2025)
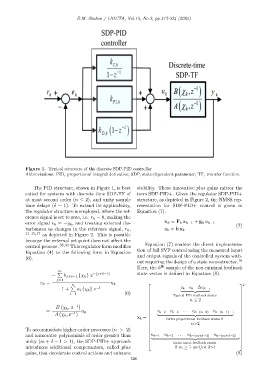
Figure 1. Typical structure of the discrete SDP-PID controller
Abbreviations: PID, proportional integral derivative; SDP, state-dependent parameter; TF, transfer function.
The PID structure, shown in Figure 1, is best stability. These innovative plus gains mirror the
suited for systems with discrete time SDP-TF of term SDP-PID+. Given the regulator SDP-PID+
at most second order (n ≤ 2), and unity sample structure, as depicted in Figure 2, the NMSS rep-
time delays (δ = 1). To extend its applicability, resentation for SDP-PID+ control is given in
the regulator structure is employed, where the ref- Equation (7).
erence signal is set to zero, i.e. r k = 0, making the
error signal e k = −y k , and treating external dis- x k = F k x k−1 + g k u k−1
(7)
turbances as changes in the reference signal, r k , y k = h x k
11–15,17
as depicted in Figure 2. This is possible
because the external set point does not affect the
control process . 33,34 This regulator form modifies Equation (7) enables the direct implementa-
tion of full SVF control using the measured input
Equation (4) to the following form in Equation
and output signals of the controlled system with-
(6).
out requiring the design of a state reconstructor. 16
Here, the k th sample of the non-minimal feedback
m
− P b j+δ−1 {χ k } z −(j+δ−1) state vector is defined in Equation (8).
j=1
e k = u k
n T
P z k e k ∆e k ,
1 + a i {χ k } z −i
i=1 (6) | {z }
Typical PID feedback states
n ≤ 2
−B χ k , z −1
= u k e k−2 e k−3 . . . e k−(n−2) e k−(n−1) ,
A (χ k , z −1 ) | {z }
x k = Extra proportional feedback states if
n>2
To accommodate higher-order processes (n > 2)
u
and numerator polynomials of order greater than k−1 u k−2 . . . u k−(m+δ−3) u k−(m+δ−2)
| {z }
unity (m + δ − 1 > 1), the SDP-PID+ approach Extra input feedback states
introduces additional compensators, called plus if m ≥ 1 and/or δ>1
gains, that decelerate control actions and enhance (8)
520