Page 149 - IJOCTA-15-3

Proportional integral derivative plus control for nonlinear discrete-time state-dependent parameter. . .

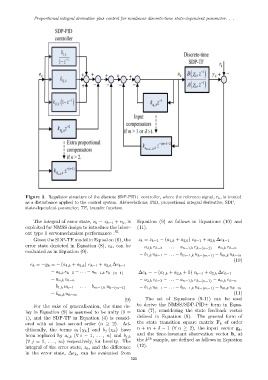
Figure 2. Regulator structure of the discrete SDP-PID+ controller, where the reference signal, r k , is treated
as a disturbance applied to the control system. Abbreviations: PID, proportional integral derivative; SDP,
state-dependent parameter; TF, transfer function

The integral of error state, z k = z k−1 + e k , is Equation (9) as follows in Equations (10) and
exploited for NMSS design to introduce the inher- (11).
ent type 1 servomechanism performance . 35
Given the SDP-TF model in Equation (6), the z k = z k−1 − (a 1,k + a 2,k ) e k−1 + a 2,k ∆e k−1
error state depicted in Equation (8), e k , can be − a 3,k e k−3 − . . . − a n−1,k e k−(n−1) − a n,k e k−n
evaluated as in Equation (9).
− b 1,k u k−1 − . . . − b m−1,k u k−(m−1) − b m,k u k−m
(10)
e k = −y k = − (a 1,k + a 2,k ) e k−1 + a 2,k ∆e k−1
− a 3,k e k−3 − . . . − a n−1,k e k−(n−1) ∆e k = − (a 1,k + a 2,k + 1) e k−1 + a 2,k ∆e k−1
− a n,k e k−n − a 3,k e k−3 − . . . − a n−1,k e k−(n−1) − a n,k e k−n
− b 1,k u k−1 − . . . − b m−1,k u k−(m−1) − b 1,k u k−1 − . . . − b m−1,k u k−(m−1) − b m,k u k−m
(11)
− b m,k u k−m
(9) The set of Equations (9-11) can be used
For the sake of generalization, the time de- to derive the NMSS/SDP-PID+ form in Equa-
lay in Equation (9) is assumed to be unity (δ = tion (7), considering the state feedback vector
1), and the SDP-TF in Equation (4) is consid- defined in Equation (8). The general form of
ered with at least second order (n ≥ 2). Ad- the state transition square matrix F k of order
ditionally, the terms a i {χ k } and b j {χ k } have n + m + δ − 1 (∀ n ≥ 2), the input vector g ,
k
and the time-invariant observation vector h, at
been replaced by a i,k (∀ i = 1, . . . , n) and b j,k th
(∀ j = 1, . . . , m) respectively, for brevity. The the k sample, are defined as follows in Equation
integral of the error state, z k , and the difference (12).
in the error state, ∆e k , can be evaluated from
521