Page 60 - MSAM-1-3

Materials Science in Additive Manufacturing Characterization of TPMS structures

the build direction. However, as shown in Figure 9E, the decreased with increasing unit size. Meanwhile, when the
orientation of the original β columnar grains was tilted, unit size was constant, the elastic modulus and maximum
and this phenomenon is more obvious in the samples after compressive stress changed very little. Comparing these
heat treatment (Figure 9F). results with those mentioned in Section 3.1, it is apparent
Figure 10 shows the phase composition of the LPBF- that the effect of the unit size and shape factor on the elastic
produced Schwarz-P structures. As shown in Figure 9A modulus and maximum compressive stress is consistent
and C, <0.5% body center β phase can be found in the with the effect on the theoretical relative density.
as-built samples, while 2% β phase exists in the samples To quantitatively investigate the relationship between
after stress relief heat treatment. The β phase is presented
as a dot between the α/α' phase. the elastic modulus and the theoretical relative density,
the Gibson-Ashby model was used to describe the
3.3. Mechanical performance behavior experimental results. As mentioned above, the coefficient
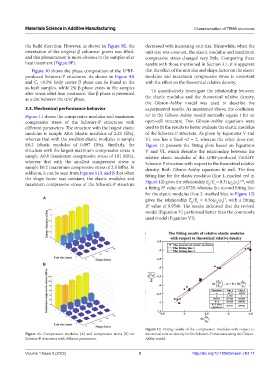
Figure 11 shows the compressive modulus and maximum n1 in the Gibson-Ashby model normally equals t for an
compressive stress of the Schwarz-P structures with open-cell structure. Two Gibson-Ashby equations were
different parameters. The structure with the largest elastic used to fit the results to better evaluate the elastic modulus
modulus is sample A0.6 (elastic modulus of 2.23 GPa), of the Schwarz-P structure. As given by Equations V and
whereas that with the smallest elastic modulus is sample VI, one has a fixed n1 = 2, whereas the other does not.
E0.2 (elastic modulus of 0.097 GPa). Similarly, the Figure 12 presents the fitting plots based on Equations
structure with the largest maximum compressive stress is V and VI, which describe the relationship between the
sample A0.8 (maximum compressive stress of 101 MPa), relative elastic modulus of the LPBF-produced Ti6Al4V
whereas that with the smallest compressive stress is Schwarz-P structure with respect to the theoretical relative
sample E0.2 (maximum compressive stress of 2.5 MPa). In density. Both Gibson-Ashby equations fit well. The first
addition, it can be seen from Figures 11A and B that when fitting line for the elastic modulus (line 1, marked red in
the shape factor was constant, the elastic modulus and Figure 12) gives the relationship E /E = 0.31(ρ /ρ ) , with
1.76
maximum compressive stress of the Schwarz-P structure p s p s
a fitting R value of 0.9729, whereas the second fitting line
2
for the elastic modulus (line 2, marked blue in Figure 12)
A gives the relationship E /E = 0.56(ρ /ρ ) , with a fitting
2
p
s
s
p
R value of 0.9546. The results indicated that the revised
2
model (Equation V) performed better than the commonly
used model (Equation VI).

B

Figure 12. Fitting results of the compression modulus with respect to
Figure 11. Compression modulus (A) and compressive stress (B) for theoretical relative density for the Schwarz-P structures using the Gibson-
Schwarz-P structures with different parameters. Ashby model.

Volume 1 Issue 3 (2022) 9 http://doi.org/10.18063/msam.v1i3.17