Page 104 - MSAM-3-4

Materials Science in Additive Manufacturing Bistable 3D-printed compliant structure

A B C

D E

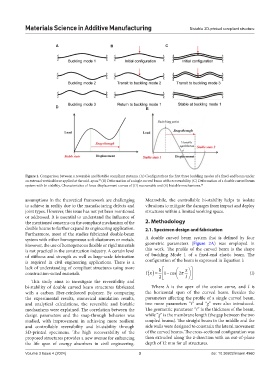
Figure 1. Comparison between a reversible and bistable compliant systems. (A) Configurations the first three buckling modes of a fixed-end beam under
an external vertical force applied at the mid-span. (B) Deformation of a single curved beam with recoverability. (C) Deformation of a double curved beam
35
36
system with bi-stability. Characteristics of force-displacement curves of (D) recoverable and (E) bistable mechanisms.
assumptions in the theoretical framework are challenging Meanwhile, the controllable bi-stability helps to isolate
to achieve in reality due to the manufacturing defects and vibrations to mitigate the damages from impact and deploy
joint types. However, this issue has not yet been mentioned structures within a limited working space.
or addressed. It is essential to understand the influence of
the mentioned concerns on the compliant mechanism of the 2. Methodology
double beams to further expand its engineering application. 2.1. Specimen design and fabrication
Furthermore, most of the studies fabricated double-beam
system with either homogeneous soft elastomers or metals. A double curved beam system that is defined by four
However, the use of homogeneous flexible or rigid materials geometric parameters (Figure 2A) was employed in
is not practical in the construction industry. A certain level this work. The profile of the curved beam is the shape
of stiffness and strength as well as large-scale fabrication of buckling Mode 1 of a fixed-end elastic beam. The
is required in civil engineering applications. There is a configuration of the beam is expressed in Equation I:
lack of understanding of compliant structures using more h   x 
construction-suited materials. lx () =  1 − cos  2π  (I)
2   l 
This study aims to investigate the reversibility and
bi-stability of double curved beam structures fabricated Where h is the apex of the cosine curve, and l is
with a carbon fiber-reinforced polymer. By comparing the horizontal span of the curved beam. Besides the
the experimental results, numerical simulation results, parameters affecting the profile of a single curved beam,
and analytical calculations, the reversible and bistable two more parameters “t” and “g” were also introduced.
mechanisms were explained. The correlation between the The geometric parameter “t” is the thickness of the beam,
design parameters and the snap-through behavior was while “g” is the membrane length (the gap between the two
studied, with improvement in achieving more resilient coupled beams). The straight beam in the middle and the
and controllable reversibility and bi-stability through side walls were designed to constrain the lateral movement
3D-printed specimens. The high recoverability of the of the curved beams. The cross-sectional configuration was
proposed structures provides a new avenue for enhancing then extruded along the z-direction with an out-of-plane
the life span of energy absorbers in civil engineering. depth of 12 mm for all structures.

Volume 3 Issue 4 (2024) 3 doi: 10.36922/msam.4960