Page 87 - MSAM-4-3

Materials Science in Additive Manufacturing Interpretable GP melt track prediction

A B

C D

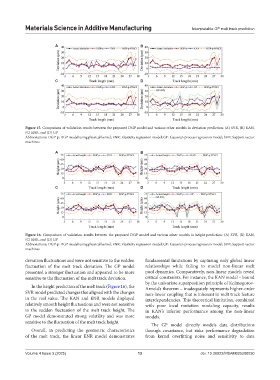
Figure 15. Comparison of validation results between the proposed DGP model and various other models in deviation prediction: (A) SVR, (B) KAN,
(C) ENR, and (D) GP
Abbreviations: DGP-p: DGP model using physical kernel; ENR: Elasticity regression model; GP: Gaussian process regression model; SVR: Support vector
machines

A B

C D

Figure 16. Comparison of validation results between the proposed DGP model and various other models in height prediction: (A) SVR, (B) KAN,
(C) ENR, and (D) GP
Abbreviations: DGP-p: DGP model using physical kernel; ENR: Elasticity regression model; GP: Gaussian process regression model; SVR: Support vector
machines
deviation fluctuations and were not sensitive to the sudden fundamental limitations by capturing only global linear
fluctuation of the melt track deviation. The GP model relationships while failing to model non-linear melt
presented a stronger fluctuation and appeared to be more pool dynamics. Comparatively, non-linear models reveal
sensitive to the fluctuation of the melt track deviation. critical constraints. For instance, the KAN model – bound
by the univariate superposition principle of Kolmogorov-
In the height prediction of the melt track (Figure 16), the Arnold’s theorem – inadequately represents higher-order
SVR model predicted changes that aligned with the changes non-linear coupling that is inherent in melt track feature
in the real value. The KAN and ENR models displayed interdependencies. This theoretical limitation, combined
relatively smooth height fluctuations and were not sensitive with poor local mutation modeling capacity, results
to the sudden fluctuation of the melt track height. The in KAN’s inferior performance among the non-linear
GP model demonstrated strong volatility and was more models.
sensitive to the fluctuation of the melt track height.
The GP model directly models data distributions
Overall, in predicting the geometric characteristics through covariance, but risks performance degradation
of the melt track, the linear ENR model demonstrates from kernel overfitting noise and sensitivity to data

Volume 4 Issue 3 (2025) 13 doi: 10.36922/MSAM025200030