Page 60 - DP-1-1

Design+ Approximate signed multipliers design approach

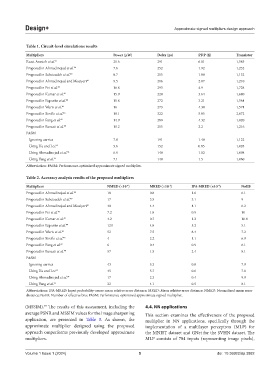
Table 1. Circuit‑level simulations results
Multipliers Power (µW) Delay (ps) PDP (fj) Transistor
Exact Arasteh et al. 31 20.6 291 6.01 1,585
Proposed in Ahmadinejad et al. 34 7.6 252 1.92 1,232
Proposed in Sabetzadeh et al. 40 8.7 215 1.88 1,132
Proposed in Ahmadinejad and Moaiyeri 41 9.5 216 2.07 1,210
Proposed in Pei et al. 42 16.8 293 4.9 1,728
Proposed in Kumar et al. 43 15.9 228 3.64 1,680
Proposed in Esposito et al. 44 11.8 272 3.21 1,564
Proposed in Waris et al. 45 16 273 4.38 1,574
Proposed in Strollo et al. 46 18.1 322 5.85 2,072
Proposed in Fang et al. 47 14.9 289 4.32 1,820
Proposed in Baraati et al. 48 10.2 215 2.2 1,216
PASM
Ignoring carries 7.8 191 1.48 1,122
Using Ha and Lee 33 5.6 152 0.85 1,028
Using Ahmadinejad et al. 34 6.9 148 1.02 1,098
Using Yang et al. 35 7.1 148 1.5 1,060
Abbreviation: PASM: Performance-optimized approximate signed multiplier.

Table 2. Accuracy analysis results of the proposed multipliers

Multipliers NMED (×10 ) MRED (×10 ) IPA‑MRED (×10 ) NoEB
‑4
‑2
‑4
Proposed in Ahmadinejad et al. 34 18 0.8 1.6 6.1
Proposed in Sabetzadeh et al. 40 17 3.5 3.1 9
Proposed in Ahmadinejad and Moaiyeri 41 40 4.4 4.1 6.2
Proposed in Pei et al. 42 7.2 1.8 0.9 10
Proposed in Kumar et al. 43 4.2 0.7 1.2 10.4
Proposed in Esposito et al. 44 120 4.8 5.2 5.1
Proposed in Waris et al. 45 52 7.5 8.4 7.2
Proposed in Strollo et al. 46 4 2.2 1.1 6.9
Proposed in Fang et al. 47 6 0.4 0.9 6.1
Proposed in Baraati et al. 48 57 1.5 2.4 8.1
PASM
Ignoring carries 43 5.3 0.8 7.9
Using Ha and Lee 33 45 5.7 0.6 7.8
Using Ahmadinejad et al. 34 17 2.3 0.4 9.9
Using Yang et al. 35 22 4.1 0.5 8.1
Abbreviations: IPA-MRED: Input probability-aware mean relative error distance; MRED: Mean relative error distance; NMED: Normalized mean error
distance; NoEB: Number of effective bits; PASM: Performance-optimized approximate signed multiplier.

(MSSIM). The results of this assessment, including the 4.4. NN applications
39
average PSNR and MSSIM values for the image sharpening This section examines the effectiveness of the proposed
application, are presented in Table 3. As shown, the multiplier in NN applications, specifically through the
approximate multiplier designed using the proposed implementation of a multilayer perceptron (MLP) for
approach outperforms previously developed approximate the MNIST dataset and GNet for the SVHN dataset. The
multipliers. MLP consists of 784 inputs (representing image pixels),

Volume 1 Issue 1 (2024) 5 doi: 10.36922/dp.3882