Page 61 - DP-1-1

Design+ Approximate signed multipliers design approach

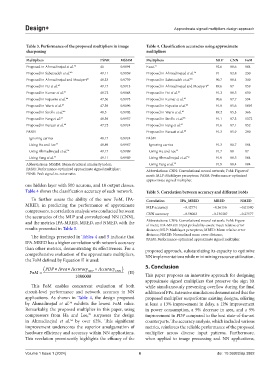
Table 3. Performance of the proposed multipliers in image Table 4. Classification accuracies using approximate
sharpening multipliers
Multipliers PSNR MSSIM Multipliers MLP CNN FoM
Proposed in Ahmadinejad et al. 34 46 0.9891 Exact 31 92.6 88.6 804
Proposed in Sabetzadeh et al. 40 49.11 0.9859 Proposed in Ahmadinejad et al. 34 91 82.8 230
Proposed in Ahmadinejad and Moaiyeri 41 48.33 0.9739 Proposed in Sabetzadeh et al. 40 90.7 88.4 340
Proposed in Pei et al. 42 49.17 0.9913 Proposed in Ahmadinejad and Moaiyeri 41 89.6 87 859
Proposed in Kumar et al. 43 48.72 0.9848 Proposed in Pei et al. 42 91.2 88.5 650
Proposed in Esposito et al. 44 47.56 0.9978 Proposed in Kumar et al. 43 90.6 87.7 594
Proposed in Waris et al. 45 47.39 0.9696 Proposed in Esposito et al. 44 91.8 85.6 1095
Proposed in Strollo et al. 46 48.5 0.9902 Proposed in Waris et al. 45 89.2 85.3 366
Proposed in Fang et al. 47 48.39 0.9957 Proposed in Strollo et al. 46 91.1 87.3 1372
Proposed in Baraati et al. 48 47.72 0.9924 Proposed in Fang et al. 47 91.6 87.1 852
PASM Proposed in Baraati et al. 48 91.3 85.9 290
Ignoring carries 48.17 0.9924 PASM
Using Ha and Lee 33 48.89 0.9967 Ignoring carries 91.3 86.7 194
Using Ahmadinejad et al. 34 49.17 0.9989 Using Ha and Lee 33 91.7 88 87
Using Yang et al. 35 49.11 0.9989 Using Ahmadinejad et al. 34 91.9 88.5 104
Abbreviations: MSSIM: Mean structural similarity index; Using Yang et al. 35 91.9 88.4 104
PASM: Performance-optimized approximate signed multiplier; Abbreviations: CNN: Convolutional neural network; FoM: Figure of
PSNR: Peak signal-to-noise ratio. merit; MLP: Multilayer perceptron; PASM: Performance-optimized
approximate signed multiplier.
one hidden layer with 500 neurons, and 10 output classes.
Table 4 shows the classification accuracy of each network. Table 5. Correlation between accuracy and different FoMs
To further assess the ability of the new FoM, IPA- Correlation IPA_MRED MRED NMED
MRED, in predicting the performance of approximate MLP accuracy −0.42774 −0.36156 −0.01540
compressors, a correlation analysis was conducted between CNN accuracy −0.58002 −0.136387 −0.27577
the accuracies of the MLP and convolutional NN (CNN),
and the metrics IPA-MRED, MRED, and NMED, with the Abbreviations: CNN: Convolutional neural network; FoM: Figure
of merit; IPA-MRED: Input probability-aware mean relative error
results presented in Table 5. distance; MLP: Multilayer perceptron; MRED: Mean relative error
The findings presented in Tables 4 and 5 indicate that distance; NMED: Normalized mean error distance;
PASM: Performance-optimized approximate signed multiplier.
IPA-MRED has a higher correlation with network accuracy
than other metrics, demonstrating its effectiveness. For a proposed approach, substantiating its capacity to optimize
comprehensive evaluation of the approximate multipliers, NN implementations while minimizing resource utilization.
the FoM defined by Equation II is used:

×
(PDP Area Accuracy × Accuracy ) 5. Conclusion
×
FoM = MLP CNN (II)
1000000 This paper proposes an innovative approach for designing
approximate signed multipliers that preserve the sign bit
This FoM enables concurrent evaluation of both while simultaneously preventing overflow during the final
circuit-level performance and network accuracy in NN addition of PPs. Extensive simulations demonstrated that the
applications. As shown in Table 4, the design proposed proposed multiplier outperforms existing designs, offering
by Ahmadinejad et al. exhibits the lowest FoM value. at least a 13% improvement in delay, a 12% improvement
34
Remarkably, the proposed multiplier in this paper, using in power consumption, a 9% decrease in area, and a 9%
compressors from Ha and Lee, surpasses the design improvement in PDP compared to the best state-of-the-art
33
in Ahmadinejad et al. by over 62%. This significant counterparts. The accuracy analysis, which included various
34
improvement underscores the superior amalgamation of metrics, reinforces the reliable performance of the proposed
hardware efficiency and accuracy within NN applications. multiplier across diverse input patterns. Furthermore,
This revelation prominently highlights the efficacy of the when applied to image processing and NN applications,

Volume 1 Issue 1 (2024) 6 doi: 10.36922/dp.3882