Page 22 - IJB-5-1

Shuai C
the unit library approach to biomimetically create porous Mathematical modeling mainly utilizes shape functions to
structures. Similar method approach was also researched construct porous scaffolds with implicit function surfaces
by Hollister et al. [60,61] by creating the internal architecture or irregular polygonal models, which breaks through the
by altering the density in the voxel dataset. Based on these geometry limitations of the traditional porous element.
early studies, Podshivalov et al. constructed microscale Among them, triply periodic minimal surface (TPMS)
[62]
structure scaffolds based on the processing of actual method uses trigonometric functions to derive a complex
micro-CT images followed by reconstructing a highly porous structure with a minimal surface, in which the
accurate geometrical model, which resembles the actual curvature at any point is zero . The TPMS structure
[58]
trabecular bone structure. Related studies showed that the also presents a periodicity in three independent directions
porous structure obtained by reverse modeling was more due to the periodic characteristic of the trigonometric
conducive to the growth of cells, which also proved the function, with no sealed cavities exist in the geometry .
[65]
superiority of irregular porous structure [63,64] . In fact, the examples of the minimal surface geometry
Although reverse modeling design can obtain the exist in nature, including beetle shells, butterfly wings,
porous structure that perfectly coincides with the natural and crustacean bones .
[66]
bone, the accuracy of the model highly depends on the Rajagopalan et al. first proposed a TPMS-based method
resolution of the image acquisition device. On top of for designing tissue scaffolds and a simple primitive
that, it needs a lot of computing resources and storage (P-type) unit . Other types of TPMS units including
[67]
space and proposes higher requirements for software diamond (D type) and gyroid (G type) were also proposed
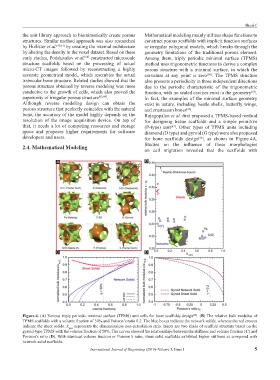
developers and users. for bone scaffolds design , as shown in Figure 4A.
[68]
2.4. Mathematical Modeling Studies on the influence of these morphologies
on cell migration revealed that the scaffolds with

A B

C D

Figure 4. (A) Various triply periodic minimal surface (TPMS) unit cells for bone scaffolds design . (B) The relative bulk modulus of
[68]
TPMS scaffolds with a volume fraction of 50% and Poisson’s ratio 0.2. The blue boxes indicate the network solids, whereas the red crosses
indicate the sheet solids. X perc represents the dimensionless non-percolation ratio. Insets are two kinds of scaffold structure based on the
gyroid-type TPMS with the volume fraction of 50%. The curves showed the relationships between the stiffness and volume fraction (C) and
Poisson’s ratio (D). With identical volume fraction or Poisson’s ratio, sheet solid scaffolds exhibited higher stiffness as compared with
network solid scaffolds.
International Journal of Bioprinting (2019)–Volume 5, Issue 1 5