Page 150 - IJOCTA-15-1

N. Tekbıyık-Ersoy / IJOCTA, Vol.15, No.1, pp.137-154 (2025)
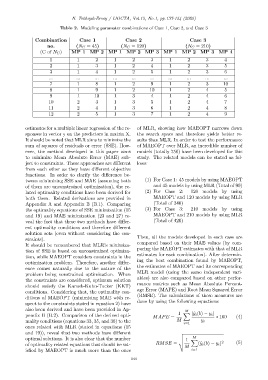
Table 2. Modeling paramater combinations of Case 1, Case 2, and Case 3

Combination Case 1 Case 2 Case 3
no. (N C = 45) (N C = 120) (N C = 210)
(C of N C ) MP 1 MP 2 MP 1 MP 2 MP 3 MP 1 MP 2 MP 3 MP 4
1 1 2 1 2 3 1 2 3 4
2 1 3 1 2 4 1 2 3 5
3 1 4 1 2 5 1 2 3 6
... ... ... ... ... ... ... ... ... ...
7 1 8 1 2 9 1 2 3 10
8 1 9 1 2 10 1 2 4 5
9 1 10 1 3 4 1 2 4 6
10 2 3 1 3 5 1 2 4 7
11 2 4 1 3 6 1 2 4 8
12 2 5 1 3 7 1 2 4 9

estimates for a multiple linear regression of the re- of MLR, showing how MAEOPT narrows down
sponses in vector y on the predictors in matrix X. the search space and therefore yields better re-
It should be noted that MLR aims to minimize the sults than MLR. In order to test the performance
sum of squares of residuals or error (SSE). How- of MAEOPT over MLR, an incredible number of
ever, the method developed in this paper aims models (totally 750) have been developed for this
to minimize Mean Absolute Error (MAE) sub- study. The related models can be stated as fol-
ject to constraints. These approaches are different lows:
from each other as they have different objective
functions. In order to clarify the difference be-
tween minimizing SSE and MAE (assuming both (1) For Case 1: 45 models by using MAEOPT
of them are unconstrained optimization), the re- and 45 models by using MLR (Total of 90)
lated optimality conditions have been derived for (2) For Case 2: 120 models by using
both them. Related derivations are provided in MAEOPT and 120 models by using MLR
Appendix A and Appendix B (B.1). Comparing (Total of 240)
the optimality equations of SSE minimization (15 (3) For Case 3: 210 models by using
and 19) and MAE minimization (23 and 27) re- MAEOPT and 210 models by using MLR
veal the fact that these two methods have differ- (Total of 420)
ent optimality conditions and therefore different
solution sets (even without considering the con-
Then, all the models developed in each case are
straints).
compared based on their MAE values (by com-
It should be remembered that MLR’s minimiza-
paring the MAEOPT estimates with that of MLR
tion of SSE is based on unconstrained optimiza-
estimates for each combination). After determin-
tion, while MAEOPT considers constraints in the
ing the best combination found by MAEOPT,
optimization problem. Therefore, another differ-
ence comes naturally due to the nature of the the estimates of MAEOPT and its corresponding
problem being constrained optimization. When MLR model (using the same independent vari-
the constraints are considered, optimum solution ables) are also compared based on other perfor-
should satisfy the Karush-Kuhn-Tucker (KKT) mance metrics such as Mean Absolute Percent-
conditions. Considering that, the optimality con- age Error (MAPE) and Root Mean Squared Error
ditions of MAEOPT (minimizing MAE with re- (RMSE). The calculations of these measures are
spect to the constraints stated in equation 2) have done by using the following equations:
also been derived and have been provided in Ap- M
1 X |ˆy i (b) − y i |
pendix B (B.2). Comparison of the derived opti- MAPE = ∗ 100 (4)
mality conditions (equations 33, 35, and 36) to the M i=1 y i
ones related with MLR (stated in equations (15
and 19)), reveal that two methods have different v
M
optimal solutions. It is also clear that the number u 1 X
u
of optimality related equations that should be sat- RMSE = t (ˆy i (b) − y i ) 2 (5)
M
isfied by MAEOPT is much more than the ones i=1
144